_S01_024_Q01.png)
Water and liquid is filled up behind a square wall of side l
Find out (a). Pressure at A, B and C
(b). Forces in part AB and BC
(c). Total force and point of application of force. (Neglect atmosphere pressure in every calculation.)
_S01_024_S01.png)
_S01_024_S02.png)
(a). As there is no liquid above 'A'
So pressure at A,pA=0
pressure at B,pB=ρgh1
Pressure at C,pC=ρgh1+2ρgh2
(b). Force at A=0
Take strip of width dx at a depth x in part AB
Pressure is equal to ρgx
force on strip=pressure×area
dF=ρgxldx
Total force upto B:Fh1∫0ρgxldx=ρgxlh212=1000×10×10×5×52=1.25×106N
In part BC for force take a elementary strip of width dx in portion BC.
pressure is equal to =ρgh1+2ρg(x−h1)
force on elementary strip=pressure×area dF=[ρgh1+2ρg(x−h1)]ldx
Total force on part BC F=∫lh1[ρgh1+2ρg(x−h1)]ldx
=[ρgh1x+2ρg[x22−h1x]]lh1l
=ρgh1h2l+2ρl[l2−h212−h1l+h21]
=ρgh1h2l+2ρgl2[l2+h21−2h1l]=ρgh1h2l+ρgl(l−h1)2
=ρgh2l[h1+h2]=ρgh2l2=1000×10×5×10×10=5×106N
(c). Total force
Taking torque about A
Total torque of force in AB=∫dF⋅x=∫h10ρgxldx.x
=[ρghlx33]h10=ρglh313=1000×10×10×1253=1.25×1073N−m
Total torque of force in BC =∫dF⋅x
On solving we get =ρgh1h2l[h1+h22]+ρgh22l[h1+2h23]
=1000×10×5×5×10[5+2.5]+1000×10×25×10[5+103]
=2.5×7.5×106+62.53×106=118.753×106
total torque =11.875×1073+1.25×1073=13.125×1073
total torque =total × distance of point of application of force from top =F.xp
6.25×106xp=13.125×1073
xp=7m
Topper's Solved these Questions
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 1 (Elasticity)
16 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 1 (Surface Tension)
21 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- ERROR AND MEASUREMENTBOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
Similar Questions
Water and liquid are filled up behind a square wall of side. Find out
a. pressures at A,B and C
b. forces in part AB and BC
c. total force and point of application of force (neglect atmospheric pressure in every calculation)
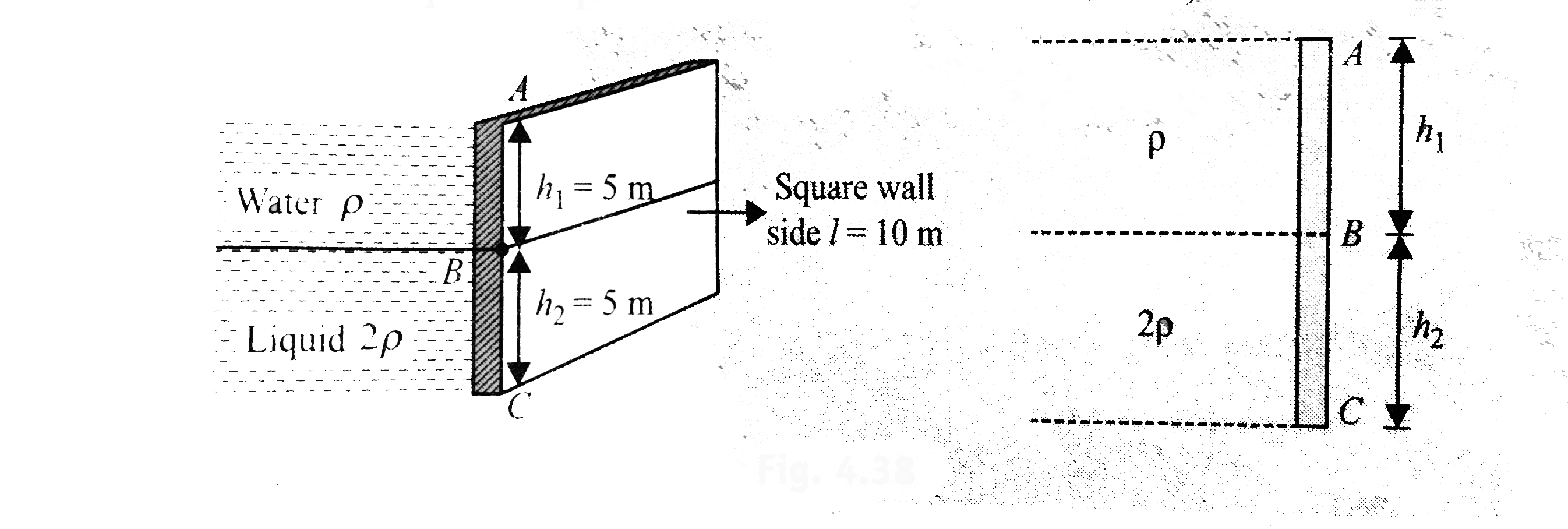
View Solution_S01_031_Q01.png)
In a given arrangement (a) find out velocity of water coming out of C
(b). Find out pressure A, B and C
View SolutionMercury is completely filled in a rectangular take of height 72 cm. The atmospheric pressure at the place is 72 cm. of Hg. Find the distance in cm of point of application from bottom of tank of the net force , on the inner surface of the side vertical wall of tank.
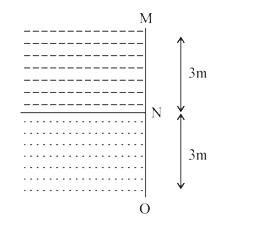
View SolutionTwo liquids of densities ρ1 and ρ2(ρ2=3ρ1) are filled up behind a square wall of side 6 m as shown in figure. Each liquid has a height of 3 m. The ratio of the forces due to these liquids exerted on upper part MN to that at the lower part NO is (Assume that the liquids are not mixing)2
View SolutionTwo liquids of densities ρ1 and ρ2(ρ2=3ρ1) are filled up behind a square wall of side 6 m as shown in figure. Each liquid has a height of 3 m. The ratio of the forces due to these liquids exerted on upper part MN to that at the lower part NO is (Assume that the liquids are not mixing)2

View Solution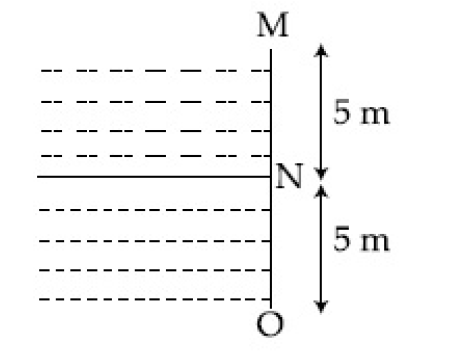 Two liquids of densities ρ1 and ρ2(ρ2=2ρ1) are filled up behind a square wall of side 10 m as shown in the figure. Each liquids has a height of 5m. The ratio of the forces due to these liqyuids exeted on upper part MN to that at the lower part NO is (Assume that the liquids are not mixing):
Two liquids of densities ρ1 and ρ2(ρ2=2ρ1) are filled up behind a square wall of side 10 m as shown in the figure. Each liquids has a height of 5m. The ratio of the forces due to these liqyuids exeted on upper part MN to that at the lower part NO is (Assume that the liquids are not mixing):
View SolutionSome liquid is filled in a cylindrical vessel of radius R. Let F1 be the force applied by the liquid on the bottom of the cylinder. Now the same liquid is poured into a vessel of uniform square cross-section of side R. Let F2 be the force applied by the liquid on the bottom of this new vessel. (Neglect atmosphere pressure). Then
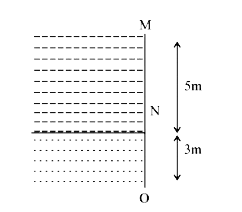
View SolutionTwo liquids of densities p1andp2(p2=6p1) are filled up behind a square wall of side 8 m as shown in figure. The liquids have height as shown. The ratio of the forces due to these liquids exerted on upper part MN to that at the lower part NO is (Assume that the liquids are not mixing)
View SolutionName a machine for each of the following use :
(a) to multiple the force,
(b) to change the point of application of force,
(c) to change the direction of force,
(d) to obtain the gain in speed.
View SolutionA liquid of density ρ is filled in a beaker of cross section S to a height H and then a cylinder of mass m and corss section s is made to float in it as shown in figure. It the atmospheric pressure is p0, find the pressure a at the top face A of the cylinder b at the botom face C of the cylinder and c. at the base B of the beaker. Can ever these three pressures be equal?

View Solution
