A block of mass M is resting on a smooth horizontal plane. One end of a uniform rope of mass M4 is fixed to the block , which pulled it in the horizontal direction by applying a force F at the other ends . The tension in the middle of the rope is
F2
F5
910F
F
The correct Answer is:C
To solve the problem of finding the tension at the midpoint of a rope attached to a block being pulled, we can follow these steps:
1. Identify the System:
- We have a block of mass M resting on a smooth horizontal plane.
- A uniform rope of mass M4 is attached to the block, and a force F is applied to the other end of the rope.
2. Draw Free Body Diagrams (FBD):
- For the block of mass M: The only horizontal forces acting on it are the tension T in the rope and the applied force F.
- For the rope: The rope can be divided into two halves. The tension at the end attached to the block is T, and the tension at the midpoint is T′.
3. Apply Newton's Second Law:
- For the block:
F−T=M⋅a(1)
- For the first half of the rope (mass = M8):
T′−T=M8⋅a(2)
- For the second half of the rope (mass = M8):
F−T′=M8⋅a(3)
4. Combine the Equations:
- From equations (1), (2), and (3), we can express F in terms of a:
- From (1): F=T+M⋅a
- From (2): T′=T+M8⋅a
- From (3): F=T′+M8⋅a
5. Substituting and Solving for Acceleration:
- Substitute T′ from equation (2) into equation (3):
F=(T+M8⋅a)+M8⋅a
F=T+M4⋅a
- Set the two expressions for F equal:
T+M⋅a=T+M4⋅a
- Rearranging gives:
M⋅a=M4⋅a
- This implies:
a=4F5M
6. Finding the Tension at Midpoint:
- Substitute a back into equation (2) to find T′:
T′=T+M8⋅4F5M
- From equation (1), we know T=M⋅a=M⋅4F5M=4F5.
- Substitute T into the equation for T′:
T′=4F5+M8⋅4F5M=4F5+4F40=4F5+F10=8F10+F10=9F10
Final Answer:
The tension at the midpoint of the rope is:
T′=9F10
- We have a block of mass M resting on a smooth horizontal plane.
- A uniform rope of mass M4 is attached to the block, and a force F is applied to the other end of the rope.
- For the block of mass M: The only horizontal forces acting on it are the tension T in the rope and the applied force F.
- For the rope: The rope can be divided into two halves. The tension at the end attached to the block is T, and the tension at the midpoint is T′.
- For the block:
F−T=M⋅a(1)
- For the first half of the rope (mass = M8):
T′−T=M8⋅a(2)
- For the second half of the rope (mass = M8):
F−T′=M8⋅a(3)
- From equations (1), (2), and (3), we can express F in terms of a:
- From (1): F=T+M⋅a
- From (2): T′=T+M8⋅a
- From (3): F=T′+M8⋅a
- Substitute T′ from equation (2) into equation (3):
F=(T+M8⋅a)+M8⋅a
F=T+M4⋅a
- Set the two expressions for F equal:
T+M⋅a=T+M4⋅a
- Rearranging gives:
M⋅a=M4⋅a
- This implies:
a=4F5M
- Substitute a back into equation (2) to find T′:
T′=T+M8⋅4F5M
- From equation (1), we know T=M⋅a=M⋅4F5M=4F5.
- Substitute T into the equation for T′:
T′=4F5+M8⋅4F5M=4F5+4F40=4F5+F10=8F10+F10=9F10
The tension at the midpoint of the rope is:
T′=9F10
Similar Questions
A block of mass m is resting one a smooth horizontal surface. One end of a uniform rope of mass m/3 is fixed to the block, which is pulled in the horizontal direction by applying force F at the other end. The tension in the middle of the rope is
View SolutionA block is lying on the horizontal frictionless surface. One end of a uniform rope is fixed to the block which is pulled in the horizontal direction by applying a force F at the other end. If the mass of the rope is half the mass of the block. The tension in the middle of the rope will be
View SolutionA block of mass 10 kg lying on a smooth horizontal surface is being pulled by means of-a rope of mass 2 kg. If a force of 36N is applied at the end of the rope, the tension at the mid point of the rope is,
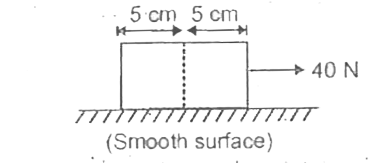
View SolutionA block of mass m as shown in figure is pulled by a force 40N. The tension at the middle of the block is
View SolutionA block of mass M is kept on as rough horizontal surface. The coefficient of static frictionbetween the block and the surface is μ. The block is to be pulled by applying a force to it. What minimum force is needed to slide the block? In which direction should this force act?
View SolutionA block B is tied to one end of a uniform rope R as shown. The mass of block is 2 kg and that of rope is 1 kg. A force F = 15 N is applies at angle 37∘ with vertical. The tension at the mid-point of rope is

View SolutionA block of mass m is placed in contact with one end of a smooth tube of mass M. A horizontal force F acts on the tube in each case (i) and (ii). Then,

View SolutionA block of mass M is pulled on a smooth horizontal table by a string making an angle θ with the horizontal as shown in figure. If the acceleration of the block is a, find the force applied by the string and by the table N on the block.

View SolutionA block of unknown mass is at rest on a rough, horizontal surface. A horizontal force F is applied to the block. The graph in the figure shows the acceleration of the block with respect to the applied force. The mass of the block is

View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m . Force F is applied at one end of rope. The force which the rope exerts on the block is:
View Solution
