A block of mass M is pulled along a horizontal frictionless surface by a rope of mass m . Force F is applied at one end of rope. The force which the rope exerts on the block is:
F/(M+m)
F should be equal to the weight of A and B
FM/(m+M)
Zero
The correct Answer is:C
To solve the problem, we need to determine the force that the rope exerts on the block when a force F is applied to the rope. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the system
We have a block of mass M and a rope of mass m on a horizontal frictionless surface. A force F is applied to one end of the rope. The entire system (rope + block) will accelerate due to the applied force.
Step 2: Calculate the total mass of the system
The total mass of the system can be expressed as:
mtotal=M+m
Step 3: Apply Newton's second law
According to Newton's second law, the net force acting on the system is equal to the total mass of the system multiplied by its acceleration:
Fnet=mtotal⋅a
Here, the net force F is the only force acting on the system. Therefore:
F=(M+m)⋅a
Step 4: Solve for acceleration
Rearranging the equation to solve for acceleration a:
a=FM+m
Step 5: Determine the force exerted by the rope on the block
The force exerted by the rope on the block can be calculated using the block's mass and the acceleration we just found. According to Newton's second law:
Frope on block=M⋅a
Substituting the expression for acceleration:
Frope on block=M⋅(FM+m)
Thus, we have:
Frope on block=M⋅FM+m
Conclusion
The force that the rope exerts on the block is:
M⋅FM+m
We have a block of mass M and a rope of mass m on a horizontal frictionless surface. A force F is applied to one end of the rope. The entire system (rope + block) will accelerate due to the applied force.
The total mass of the system can be expressed as:
mtotal=M+m
According to Newton's second law, the net force acting on the system is equal to the total mass of the system multiplied by its acceleration:
Fnet=mtotal⋅a
Here, the net force F is the only force acting on the system. Therefore:
F=(M+m)⋅a
Rearranging the equation to solve for acceleration a:
a=FM+m
The force exerted by the rope on the block can be calculated using the block's mass and the acceleration we just found. According to Newton's second law:
Frope on block=M⋅a
Substituting the expression for acceleration:
Frope on block=M⋅(FM+m)
Thus, we have:
Frope on block=M⋅FM+m
The force that the rope exerts on the block is:
M⋅FM+m
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III28videos
NEWTONS LAWS OF MOTION
- BOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-I52videos
NEWTONS LAWS OF MOTION
- BOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)4videos
NEWTON'S LAWS OF MOTION & FRICTION
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)24videos
RACE
Similar Questions
A block of mass M is pulled along a horizontal frictionless surface by a rope of mass m. If a force P is applied at the free end of the rope, the force exerted by the rope on the block is
View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m as shown in A horizontal force F is applied to one end of the rope. Find
(a) the acceleration of the rope and block
(b) the force that the rope exerts on the block
(c) the tension in the rope at its mid point
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass M is pulled along horizontal firctionless surface by a rop of mass m. Force P is applied at one end of rope. The force which the rope exerts on the block is
APM−mBPM(m+M)CPM(m+M)DPMM−m
A block of mass Mis pulled vertically upward through a rope of mass m by applying force F on one end of the rope. What force does the rope exert on the block?
View SolutionA block of mass 10 kg lying on a smooth horizontal surface is being pulled by means of-a rope of mass 2 kg. If a force of 36N is applied at the end of the rope, the tension at the mid point of the rope is,
View SolutionA block of mass M is pulled along a horizontal surface by applying a force at angle θ with the horizontal. The friction coefficient between the block and the surface is μ. If the block travels at a uniform velocity, find the work done by this applied force during a displacement d of the block.
View SolutionA block of mass M is pulled along a horizontal surface by applying a force at angle θ with the horizontal. The friction coefficient between the block and the surfasce is μ. If the block travels at a uniform velocity, find the work donen by this applied force during a displacement d of the blcok.
View SolutionA block of unknown mass is at rest on a rough, horizontal surface. A horizontal force F is applied to the block. The graph in the figure shows the acceleration of the block with respect to the applied force. The mass of the block is
 View Solution
View SolutionA block of mass √3/10kg is placed on a rough horizontal surface as shown in the figure. A force of 1N is applied at one end of the block and the block remains stationary. The normal force exerted by the sruface on the block acts(g=10m/s2)
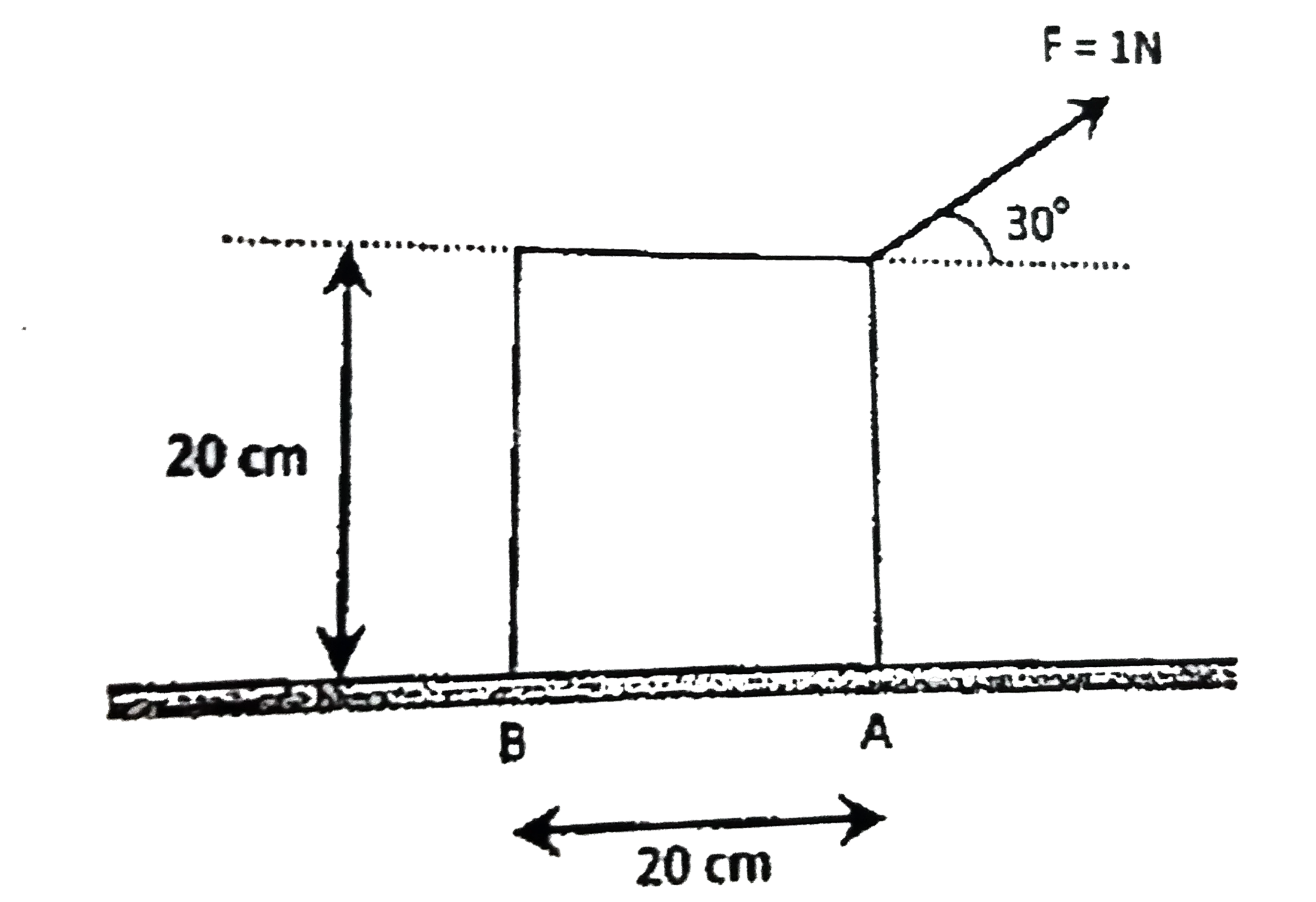 View Solution
View SolutionSTATEMENT-1: A block is pulled along a horizontal frictionless surface by a thick rope. The tension in the rope will not always be the same at all points on it.
because
STATEMENT-2: the tension in the rope depends on the acceleration of the block rope system and the mass of the rope.View Solution

