water is flowing through a tube of non-uniform cross-section. If the radii of the tube at the entrance and the exit are in the ratio 3:2 then the ratio of the velocites of flow of watern at the entrance and the exit is
1:1
4:9
9:4
8:27
The correct Answer is:B
To solve the problem, we will use the principle of continuity for fluid flow, which states that the mass flow rate must remain constant in a tube of varying cross-section. This means that the product of the cross-sectional area and the velocity of the fluid must be the same at any two points along the tube.
1. Identify the Given Ratios:
- The ratio of the radii at the entrance (R1) and the exit (R2) of the tube is given as 3:2.
- Therefore, we can express this as:
R1R2=32
2. Calculate the Areas:
- The area (A) of a circular cross-section is given by the formula:
A=πR2
- Thus, the area at the entrance (A1) and the exit (A2) can be expressed as:
A1=πR12andA2=πR22
3. Apply the Continuity Equation:
- According to the continuity equation:
A1⋅V1=A2⋅V2
- Substituting the areas we calculated:
πR12⋅V1=πR22⋅V2
- The π cancels out:
R12⋅V1=R22⋅V2
4. Rearranging for Velocity Ratio:
- Rearranging the equation gives us:
V1V2=R22R12
5. Substituting the Radius Ratio:
- We know R1R2=32, so:
R2R1=23
- Squaring both sides:
(R2R1)2=(23)2=49
6. Final Velocity Ratio:
- Substituting this back into the velocity ratio:
V1V2=49
- Therefore, the ratio of the velocities of flow of water at the entrance and the exit is:
V1:V2=4:9
Final Answer:
The ratio of the velocities of flow of water at the entrance and the exit is 4:9.
- The ratio of the radii at the entrance (R1) and the exit (R2) of the tube is given as 3:2.
- Therefore, we can express this as:
R1R2=32
- The area (A) of a circular cross-section is given by the formula:
A=πR2
- Thus, the area at the entrance (A1) and the exit (A2) can be expressed as:
A1=πR12andA2=πR22
- According to the continuity equation:
A1⋅V1=A2⋅V2
- Substituting the areas we calculated:
πR12⋅V1=πR22⋅V2
- The π cancels out:
R12⋅V1=R22⋅V2
- Rearranging the equation gives us:
V1V2=R22R12
- We know R1R2=32, so:
R2R1=23
- Squaring both sides:
(R2R1)2=(23)2=49
- Substituting this back into the velocity ratio:
V1V2=49
- Therefore, the ratio of the velocities of flow of water at the entrance and the exit is:
V1:V2=4:9
The ratio of the velocities of flow of water at the entrance and the exit is 4:9.
Similar Questions
Water is flowing through a horizontal tube of non-uniform cross-section. At a place, the radius of the tube is 1.0cm and the velocity of water is 2m/s. What will be the velocity of water where the radius of the pipe is 2.0cm?
View SolutionA stready current i is flowing through a conductor of uniform cross-section. Any segment of the conductor has
View SolutionCurrent is flowing through a wire of non-uniform cross section. Cross section of wire at A is les than the cross section of wire at B. Then match the following
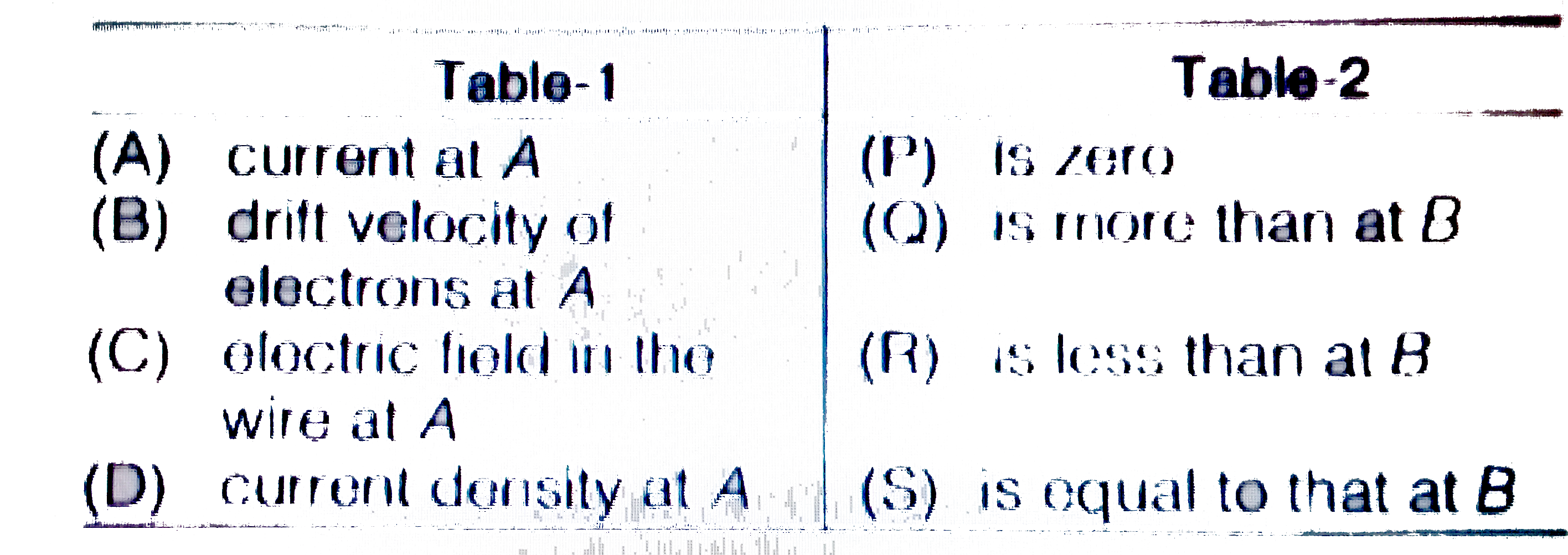
View SolutionA liquid is flowing through a pipe of non-uniform cross-section. At a point where area of cross-section of the pipe is less, match the following columns.

View SolutionWhen a steady current flows through a metal conductor of non-uniform cross-section , then drift velocity is
View SolutionThe water flowing through the same tube having two different cross section areas has different flow rates .
View SolutionWater is flowing steadily through a horizontal pipe of non - uniform cross - section . If the velocity of water cross - section is 0.02m2 is 2m/s , what is the velocity of water at another point where the cross - section is 0.01m2 ?
View SolutionHeat is flowing through two cylindrical rods of the same material . The diameters of the rods are in the ratio 1:2 and the lengths in the ratio 2:1.If the temperature difference between the ends be the same ,then the ratio of the rate of flow if heat through them will be ?
View SolutionAlcohol flows through two capillary tubes under a pressure lead. The diameter of the two tubes are in the ratio of 4:1 and the length are in the ratio of 1:4. Compare the rate of flow of alcohol through the two tubes.
View SolutionWater is flowing through a long horizontal tube. Let PAandPB be the pressures at two points A and B of the tube
View Solution