One end of a massless spring of spring constant 100 N/m and natural length 0.5 m is fixed and the other end is connected to a particle of mass 0.5 kg lying on as frictionless horizontal table. The spring remains horizontal. If the mass is made to rotate at an angular velocity of 2 rad/s, find the elongation of the spring.
To solve the problem, we need to find the elongation of the spring when a mass is rotating at a certain angular velocity. Here’s the step-by-step solution:
Step 1: Understand the system
We have a mass m=0.5kg attached to a spring with a spring constant k=100N/m. The natural length of the spring is L0=0.5m. The mass is rotating with an angular velocity ω=2rad/s.
Step 2: Set up the equations
When the mass rotates, the spring stretches by an elongation x. The total length of the spring when stretched is:
L=L0+x=0.5+x
Step 3: Identify the forces
The centripetal force required to keep the mass moving in a circle is provided by the spring force. The spring force can be expressed as:
Fspring=kx
The centripetal force needed for circular motion is given by:
Fcentripetal=mω2R
where R is the radius of the circular path, which is equal to the length of the spring when stretched:
R=L=0.5+x
Step 4: Set the forces equal
Equating the spring force to the centripetal force gives us:
kx=mω2(0.5+x)
Step 5: Substitute known values
Substituting the known values into the equation:
100x=0.5⋅(22)⋅(0.5+x)
100x=0.5⋅4⋅(0.5+x)
100x=2(0.5+x)
100x=1+2x
Step 6: Rearrange the equation
Rearranging gives:
100x−2x=1
98x=1
Step 7: Solve for x
Now, solve for x:
x=198m
Conclusion
The elongation of the spring is:
x≈0.0102m or 1.02cm
We have a mass m=0.5kg attached to a spring with a spring constant k=100N/m. The natural length of the spring is L0=0.5m. The mass is rotating with an angular velocity ω=2rad/s.
When the mass rotates, the spring stretches by an elongation x. The total length of the spring when stretched is:
L=L0+x=0.5+x
The centripetal force required to keep the mass moving in a circle is provided by the spring force. The spring force can be expressed as:
Fspring=kx
The centripetal force needed for circular motion is given by:
Fcentripetal=mω2R
where R is the radius of the circular path, which is equal to the length of the spring when stretched:
R=L=0.5+x
Equating the spring force to the centripetal force gives us:
kx=mω2(0.5+x)
Substituting the known values into the equation:
100x=0.5⋅(22)⋅(0.5+x)
100x=0.5⋅4⋅(0.5+x)
100x=2(0.5+x)
100x=1+2x
Rearranging gives:
100x−2x=1
98x=1
Now, solve for x:
x=198m
The elongation of the spring is:
x≈0.0102m or 1.02cm
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Objective -1
16 Videos
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Objective -2
6 Videos
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Question for short Answer
10 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -2
11 Videos
- FLUID MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - All Questions
90 Videos
Similar Questions
A spring of force constant 1200Nm−1 is mounted on a horizontal table and a mass of 3.0 kg of attached to the free and of the spring. The mass is made to rotate with an angular velocity of 10 rad/s. What is the elongation produced in the spring if its unstretched length is 60 cm ?
View SolutionOne end of a light spring of spring constant k is fixed to a wall and the other end is tied to a block placed on a smooth horizontal surface. In a displacement, the work by the spring is 12kx2. The possible cases are
View SolutionA particle of mass m is fixed to one end of a massless spring of spring constant k and natural length l0. The system is rotated about the other end of the spring with an angular velocity ω ub gravity-free space. The final length of spring is
View SolutionA massive spring of mass m and length l is fixed at one end and the other end is given a velocity v such that speed of spring particles increases increases linearly. Find the kinetic energy of spring.

View SolutionOne end of a light spring of spring constant k is fixed to a wall and the other end is tied to a block placed on a smooth horizontal surface. In a displacment, the work done by the spring is +(12)kx2. The possible cases are.
View SolutionOne end of a light spring of spring constant k is fixed to a wall and the other end is tied to a block placed on a smooth horizontal surface. In a displacement, the work done by the spring is +(12)kx2. The possible cases are.
View Solution
A small block of mass m is fixed at upper end of a massive vertical spring of spring constant k=2mgL and natural length 10L The lower end of spring is free and is at a height L from fixed horizontal floor as shown. The spring is initially unstressed and the spring block system is released from rest in the shown position.
Q. Till the blocks reaches its lowest position for the first time, the time duration for which the spring remains compressed is
View SolutionA block of mass m is connected at one end of spring fixed at other end having natural length l0 and spring constant K. The block is rotated with constant angular speed (ω) in gravity free space. Find the elongation in spring.
View SolutionTwo blocks of masses m and m' are connected by a light spring on a horizontal frictionless table . The spring is compressed and then released . Find the ratio of acceleration of masses .
View SolutionOne end of a light spring of natural length 4m and spring constant 170 N/m is fixed on a rigid wall and the other is fixed to a smooth ring of mass 12 kg which can slide without friction in a verical rod fixed at a distance 4 m from the wall. Initially the spring makes an angle of 37∘ with the horizontal as shown in figure. When the system is released from rest, find the speed of the ring when the spring becomes horizontal.
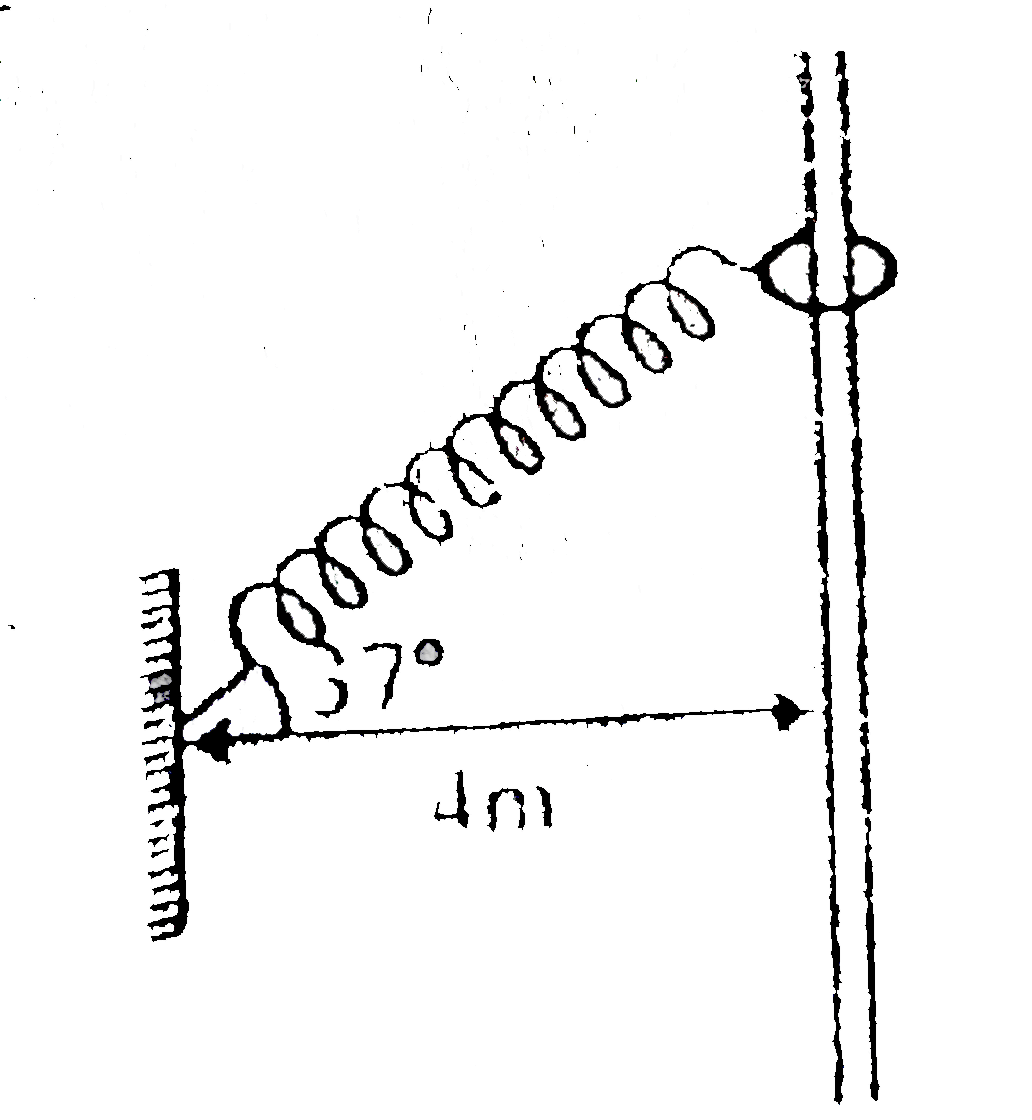
View Solution
