A mete bridge is used to determine the resistance of an unknown wire by measuring the balance point length l. If the wire is replaced by another wire of same material but with double the length and half the thickness the balancing point is expected to be
18l
14l
8l
16l
The correct Answer is:C
To solve the problem, we need to determine the new balancing point length L′ when the wire is replaced by another wire of the same material, but with double the length and half the thickness.
1. Understanding the Initial Setup:
- Let the original wire have a length L and a thickness r (radius).
- The resistance R of the wire can be expressed as:
R=ρLA
where A is the cross-sectional area of the wire.
2. Calculating the Cross-Sectional Area:
- The cross-sectional area A of a wire with radius r is given by:
A=πr2
- Therefore, the resistance can be rewritten as:
R=ρLπr2
3. Replacing the Wire:
- The new wire has double the length, so L′=2L.
- The thickness (radius) is half, so the new radius r′=r2.
4. Calculating the New Cross-Sectional Area:
- The new cross-sectional area A′ is:
A′=π(r′)2=π(r2)2=πr24=πr24
5. Calculating the New Resistance:
- The resistance R′ of the new wire can now be calculated:
R′=ρL′A′=ρ(2L)πr24=8ρLπr2
- Since the original resistance R is ρLπr2, we can express R′ in terms of R:
R′=8R
6. Using the Meter Bridge Principle:
- According to the meter bridge principle, the ratio of the resistances is equal to the ratio of the lengths:
RR′=LL′
- Substituting R′=8R:
R8R=LL′⟹18=LL′
7. Finding the New Balancing Point:
- Rearranging gives:
L′=8L
Conclusion:
The new balancing point L′ when the wire is replaced is expected to be 8L.
- Let the original wire have a length L and a thickness r (radius).
- The resistance R of the wire can be expressed as:
R=ρLA
where A is the cross-sectional area of the wire.
- The cross-sectional area A of a wire with radius r is given by:
A=πr2
- Therefore, the resistance can be rewritten as:
R=ρLπr2
- The new wire has double the length, so L′=2L.
- The thickness (radius) is half, so the new radius r′=r2.
- The new cross-sectional area A′ is:
A′=π(r′)2=π(r2)2=πr24=πr24
- The resistance R′ of the new wire can now be calculated:
R′=ρL′A′=ρ(2L)πr24=8ρLπr2
- Since the original resistance R is ρLπr2, we can express R′ in terms of R:
R′=8R
- According to the meter bridge principle, the ratio of the resistances is equal to the ratio of the lengths:
RR′=LL′
- Substituting R′=8R:
R8R=LL′⟹18=LL′
- Rearranging gives:
L′=8L
The new balancing point L′ when the wire is replaced is expected to be 8L.
Similar Questions
Knowledge Check
A wire is stretched by 10 mm when it is pulled bya certain force. Another wire of the same material but double the length and double the diameter is stretched by the same force. The elongation of the second wire is
A5 mmB10 mmC20 mmD40 mmIf the work done in stretching a wire by 1mm is 2J, then work necessary for stretching another wire of same material but with double radius of cross -section and half of the length by 1mm is
A16JB8JC4JD14JA wire of length L and radius r is clamped at one end. On stretching the other end of the wire with a force F, the increase in its length is 1. If another wire of same material but of length 2L and radius 2r is stretched with a force 2F, the increase in its leagth will be
Al4Bl2ClD2l
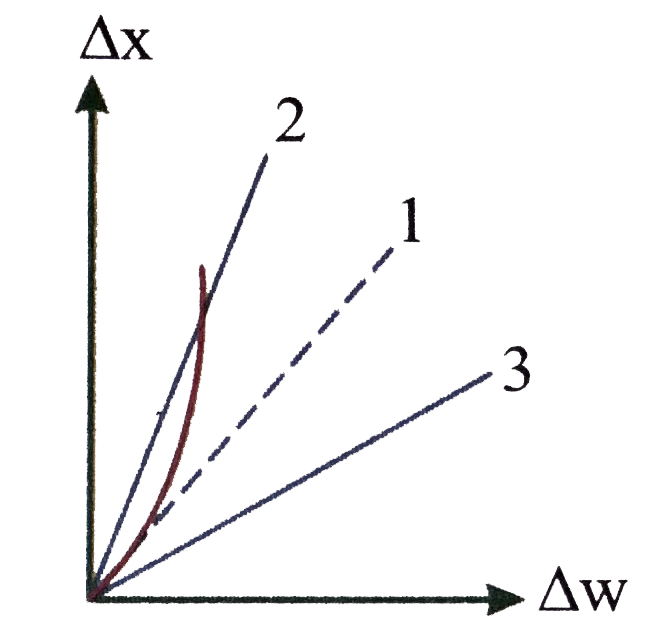
In the experiment, the curve between ΔX and ΔW is shown as dotted line (l). If we use an another wire of same material, but with double length and double radius. Which of the curve is expected.
View SolutionIn a wire of length L, the increase in its length is l. If the length is reduced to half, the increase in its length will be
View SolutionDetermination of unknonw resistance in metre bridge is most accurate , when the balancing length is
View SolutionA wire of length L and radius a rigidlyl fixed at one end. On stretching the other end of the wire with a force F, the increase in its length is L, if another wire of same material but of length 2 L and radius 2 a is stretched with a force 2 F, the increase in its length will be
View SolutionFour wires made of same material have different lengths and radii, the wire having more resistance in the following case is
View Solution