Two springs of constants k1 and k2 have equal maximum velocities, when executing simple harmonic motion. The ratio of their amplitudes (masses are equal) will be
(k1k2)12
(k1k2)
(k2k1)
(k2k1)12
The correct Answer is:D
To solve the problem, we need to analyze the relationship between the maximum velocities of two springs executing simple harmonic motion (SHM) and their respective amplitudes. Given that the masses are equal, we can derive the ratio of their amplitudes based on their spring constants.
1. Understanding the Kinetic Energy in SHM:
The kinetic energy (KE) of an object executing SHM is given by the formula:
KE=12mv2max
where m is the mass and vmax is the maximum velocity.
2. Understanding the Potential Energy in SHM:
The potential energy (PE) stored in a spring when it is stretched or compressed is given by:
PE=12ka2
where k is the spring constant and a is the amplitude of the motion.
3. Setting Up the Equations:
For the two springs with constants k1 and k2, and amplitudes a1 and a2, we can write the kinetic energy equations as follows:
- For spring 1:
12mv2max=12k1a21
- For spring 2:
12mv2max=12k2a22
4. Equating the Kinetic Energies:
Since the maximum velocities are equal for both springs, we can set the two equations equal to each other:
12k1a21=12k2a22
5. Simplifying the Equation:
Canceling the 12 from both sides gives:
k1a21=k2a22
6. Finding the Ratio of Amplitudes:
Rearranging the equation to find the ratio of the amplitudes a1a2:
a21a22=k2k1
Taking the square root of both sides, we get:
a1a2=√k2k1
7. Final Answer:
Thus, the ratio of their amplitudes is:
a1a2=√k2k1
Conclusion:
The final answer is a1a2=√k2k1.
The kinetic energy (KE) of an object executing SHM is given by the formula:
KE=12mv2max
where m is the mass and vmax is the maximum velocity.
The potential energy (PE) stored in a spring when it is stretched or compressed is given by:
PE=12ka2
where k is the spring constant and a is the amplitude of the motion.
For the two springs with constants k1 and k2, and amplitudes a1 and a2, we can write the kinetic energy equations as follows:
- For spring 1:
12mv2max=12k1a21
- For spring 2:
12mv2max=12k2a22
Since the maximum velocities are equal for both springs, we can set the two equations equal to each other:
12k1a21=12k2a22
Canceling the 12 from both sides gives:
k1a21=k2a22
Rearranging the equation to find the ratio of the amplitudes a1a2:
a21a22=k2k1
Taking the square root of both sides, we get:
a1a2=√k2k1
Thus, the ratio of their amplitudes is:
a1a2=√k2k1
The final answer is a1a2=√k2k1.
Similar Questions
Two springs, of spring constants k1 and K2, have equal highest velocities, when executing SHM. Then, the ratio of their amplitudes (given their masses are in the ratio 1:2) will be
View SolutionThe maximum velocity of a particle, excuting simple harmonic motion with an amplitude 7mm, is 4.4m/s The period of oscillation is.
View SolutionTwo particle A and B of equal masses are suspended from two massless springs of spring constants k1 and k2, respectively. If the maximum velocities, during oscillations are equal, the ratio of amplitude of A and B is (4/3)×1000kg/m3. What relationship betwen t and t0 is ture?
View SolutionTwo spring mass systeam have equal mass and spring constant k1 and k2. If the maximum velocities in two systeams are equal then ratio of amplitudes of 1st to that of 2nd is :
View SolutionTwo springs of spring constantsK1 and K2 are joined in series. The effective spring constant of the combination is given by
View SolutionTwo springs of spring constantsK1 and K2 are joined in series. The effective spring constant of the combination is given by
View SolutionTwo bodies A and B of equal mass are suspended from two separate massless springs of spring constant k1andk2 respectively. If the bodies Oscillate vertically such that their maximum velocities are equal, the ratio of the amplitude of A to that of B is
View SolutionTwo bodies (M) and (N) of equal masses are suspended from two separate massless springs of spring constants (k_1) and (k_2) respectively. If the two bodies oscillate vertically such that their maximum velocities are equal, the ratio of the amplitude of vibration of (M) to the of (N) is.
View Solution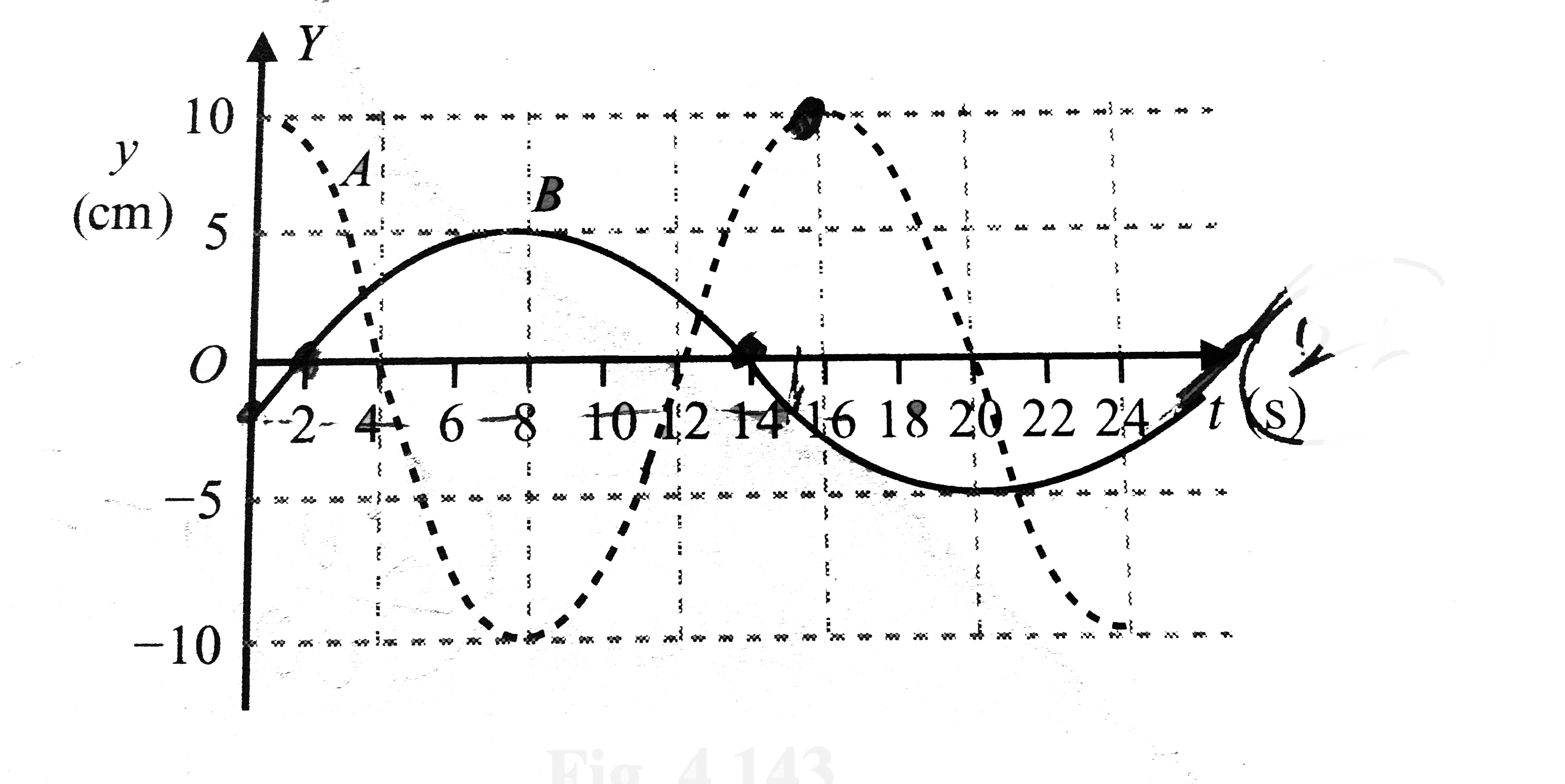
The following figure shows the displacement versus time graph for two particles A and B executing simple harmonic motions. The ratio of their maximum velocities is
View SolutionTwo bodies P and Q of equal masses are suspended from two separate massless springs of force constants k1 and k2 respectively. If the two bodies oscillate vertically such that their maximum velocities are equal. The ratio of the amplitude of P to that of Q is
View Solution
