In a series LCR circuit the rms voltage across the inductance , capacitance and resistance are respectively 4 V, 8 V and 5 V . The RMS voltage of the AC source in the circuit is
17 V
13 V
5 V
6.4 V
The correct Answer is:D
To find the RMS voltage of the AC source in a series LCR circuit where the RMS voltages across the inductance (VL), capacitance (VC), and resistance (VR) are given as 4 V, 8 V, and 5 V respectively, we can follow these steps:
1. Identify the Given Values:
- Voltage across the resistance (VR) = 5 V
- Voltage across the capacitance (VC) = 8 V
- Voltage across the inductance (VL) = 4 V
2. Understand the Phasor Relationships:
- In a series LCR circuit, the current (I) is the same through all components.
- The voltage across the resistor (VR) is in phase with the current.
- The voltage across the inductor (VL) leads the current by 90 degrees.
- The voltage across the capacitor (VC) lags behind the current by 90 degrees.
3. Set Up the Equation for the RMS Voltage of the AC Source (V):
- The total voltage (V) can be calculated using the formula:
V=√VR2+(VC−VL)2
- This formula accounts for the phase differences between the voltages.
4. Substitute the Given Values:
- Substitute VR = 5 V, VC = 8 V, and VL = 4 V into the equation:
V=√52+(8−4)2
5. Calculate the Values:
- Calculate VR2:
VR2=52=25
- Calculate (VC−VL)2:
(VC−VL)=(8−4)=4⇒(VC−VL)2=42=16
6. Combine the Results:
- Now substitute back into the equation:
V=√25+16=√41
7. Calculate the Final Result:
- Find the square root:
V≈6.4V
Conclusion:
The RMS voltage of the AC source in the circuit is approximately 6.4 V.
- Voltage across the resistance (VR) = 5 V
- Voltage across the capacitance (VC) = 8 V
- Voltage across the inductance (VL) = 4 V
- In a series LCR circuit, the current (I) is the same through all components.
- The voltage across the resistor (VR) is in phase with the current.
- The voltage across the inductor (VL) leads the current by 90 degrees.
- The voltage across the capacitor (VC) lags behind the current by 90 degrees.
- The total voltage (V) can be calculated using the formula:
V=√VR2+(VC−VL)2
- This formula accounts for the phase differences between the voltages.
- Substitute VR = 5 V, VC = 8 V, and VL = 4 V into the equation:
V=√52+(8−4)2
- Calculate VR2:
VR2=52=25
- Calculate (VC−VL)2:
(VC−VL)=(8−4)=4⇒(VC−VL)2=42=16
- Now substitute back into the equation:
V=√25+16=√41
- Find the square root:
V≈6.4V
The RMS voltage of the AC source in the circuit is approximately 6.4 V.
Similar Questions
Knowledge Check
In a series LCR circuit the voltage across an inductor, capacitor and resistor are 20 V, 20 V and 40 V respectively. The phase difference between the applied voltage and the current in the circuit is
A30∘B45∘C60∘D0∘In a series LCR circuit, the voltage across the resistance, capacitance and inductance is 10 V each. If the capacitance is short circuited, the voltage across the inductance will be
A10VB10√2VC10√2VD20V
In a series L-C-R circuit the voltage across resistance , capacitance and inductance is 10 V each. If the capacitance is short circuited, the voltage across the inductance will be
View SolutionIn the circuit the rms value of voltage across the capacitor C, inductor L and resister R1 are respectively 5√5V, 10 V and 5V. Then the peak voltage a cross R2 is
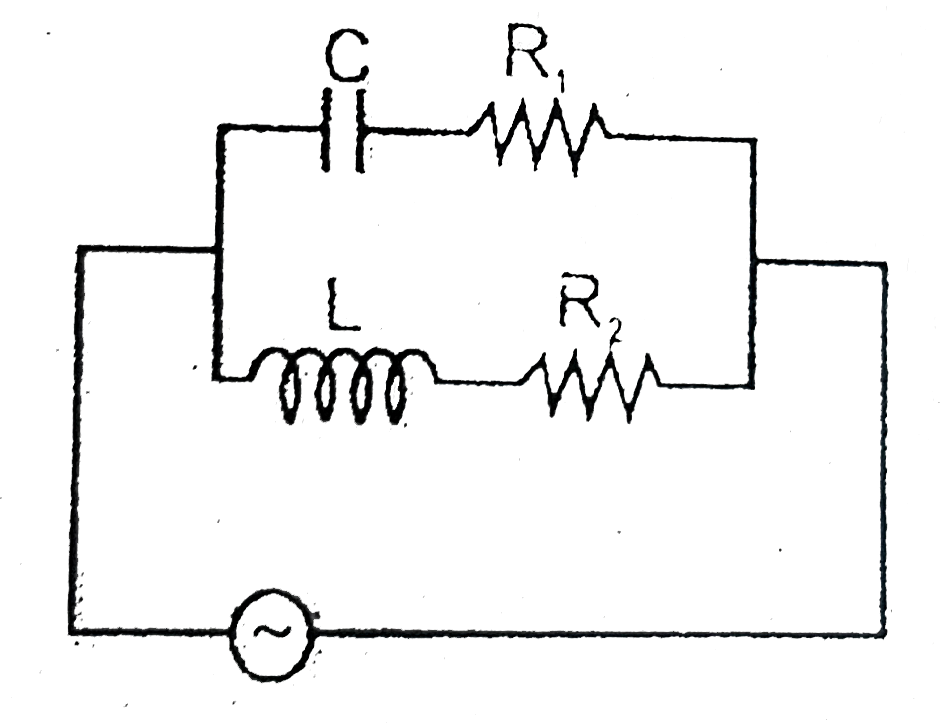
View SolutionIn a series RLC circuit the r.m.s. voltage across the resistor and the inductor are respectively 400 V and 700 V. If the equation for the applied Voltage is ε=500√2sinωt. then the peak voltage across the capacitor is

View SolutionIn an ac circuit the potential differences across an inductance and resistance joined in series are, respectively, 16 V and 20 V. The total potential difference across the circuit is
View SolutionIn an ac circuit the potential differences across an inductance and resistance joined in series are, respectively, 16 V and 20 V. The total potential difference across the circuit is
View SolutionIn a series LCR circuit, the voltages across an inductor, a capacitor and a resistor are 30 V, 30 V, 60 V respectively. What is the phase difference between the applied voltage and the current in the circuit ?
View Solution
