The block of mass 3M is attached to the pulley system as shown in the figure. At t = 0, particle M falling vertically , strikes the block 3 M with velocity 8 m s−1 and sticks to it. The speed of the combined mass just after the collision is
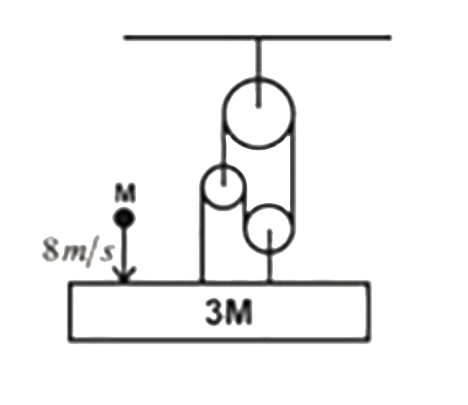
8ms−1
10ms−1
5ms−1
2ms−1
The correct Answer is:D
Step by step video & image solution for The block of mass 3M is attached to the pulley system as shown in the figure. At t = 0, particle M falling vertically , strikes the block 3 M with velocity 8 m s^(-1) and sticks to it. The speed of the combined mass just after the collision is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
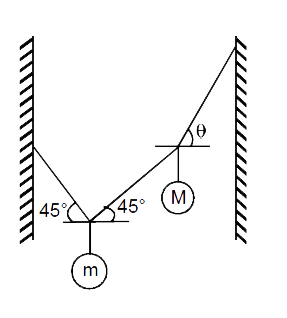
Two masses m and M are attached to the strings as shown in the figure. If the system is in equilibrium, then
View SolutionA block of mass m is attached with two strings as shown in figure .Draw the free body diagram of the block.

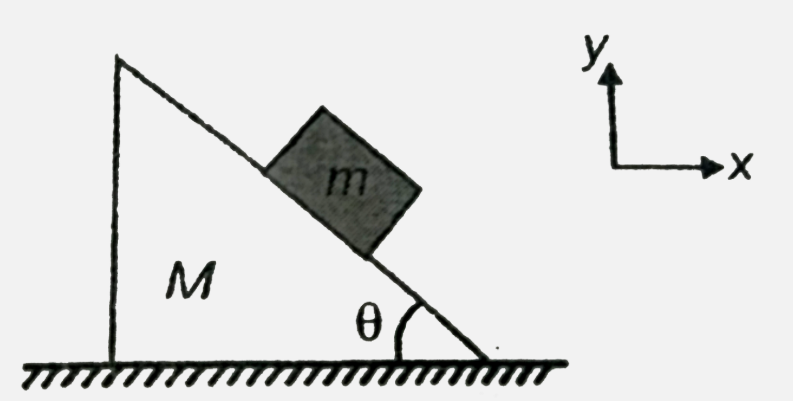
View SolutionA block of mass m is placed on a smooth wedge of mass M, as shown in the figure . Just after placiing block m over wedge M.
View SolutionA blocked of mass m is attached with two strings as shown in figure .Draw the free body diagram of the block.

View SolutionA particle of mass 2m moving with velocity v strikes a stationary particle of mass 3m and sticks to it . The speed of the system will be
View SolutionTwo masses 2m and m are connected by an inextensible light string. The string is passing over a light frictionless pulley. The mass 2m is resting on a surface and mass m is hanging in air as shown in the figure. A particle of mass m strikes the mass m from below and with a velocity v0 and sticks to it. In another case a particle of mass m strikes the mass m with a velocity v) from top and sticks to it. Calculate the ratio of velocities of mass m just after collision in first and second case.
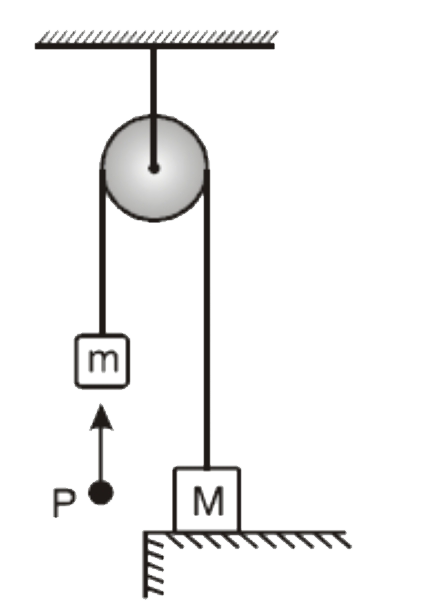
View SolutionA light inelastic thread passes over a small frictionless pulley. Two blocks of masses m = 1 kg and M = 3 kg, respectively, are attached with the thread and heavy block rests on a surface. A particle P of mass 1 kg moving upward with a velocity of 10ms−1 collides with the lighter block and sticks to it. The speed of the bigger block just after the string is taut will be [g=10ms−2]
View SolutionA block A of mass 2m is hanging from a vertical massless spring of spring constant k and is in equilibrium. Another block B of mass m strikes the block A with velocity u and sticks to it as shown in the figure. The magnitude of the acceleration of the combined system of the blocks just after the collision is
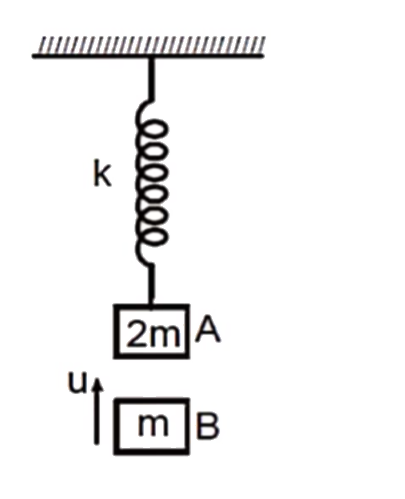
View SolutionA system is shown in the figure. Block A moves with velocity 10m/s. The speed of the mass B will be :
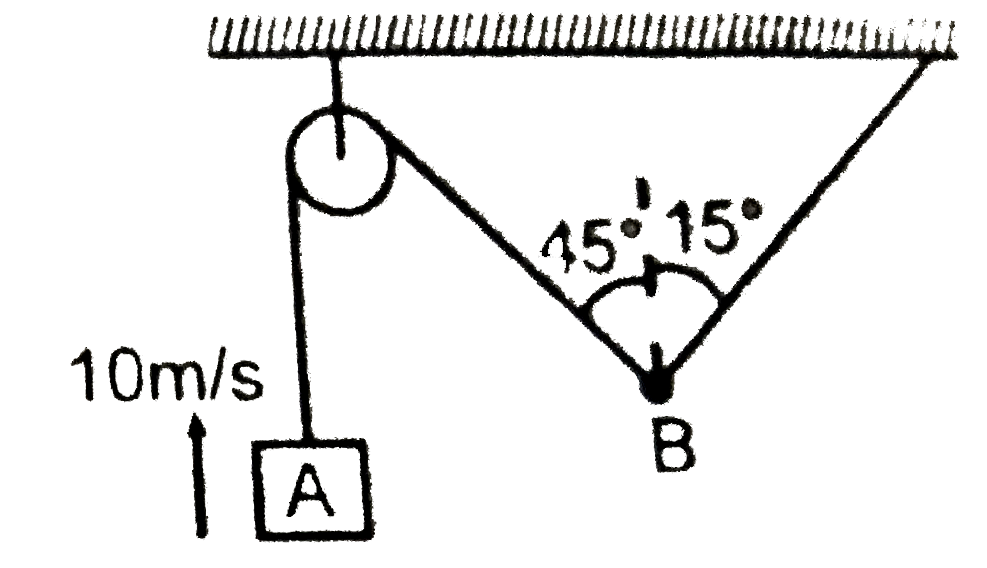
View Solution
Two blocks of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is :
View Solution
