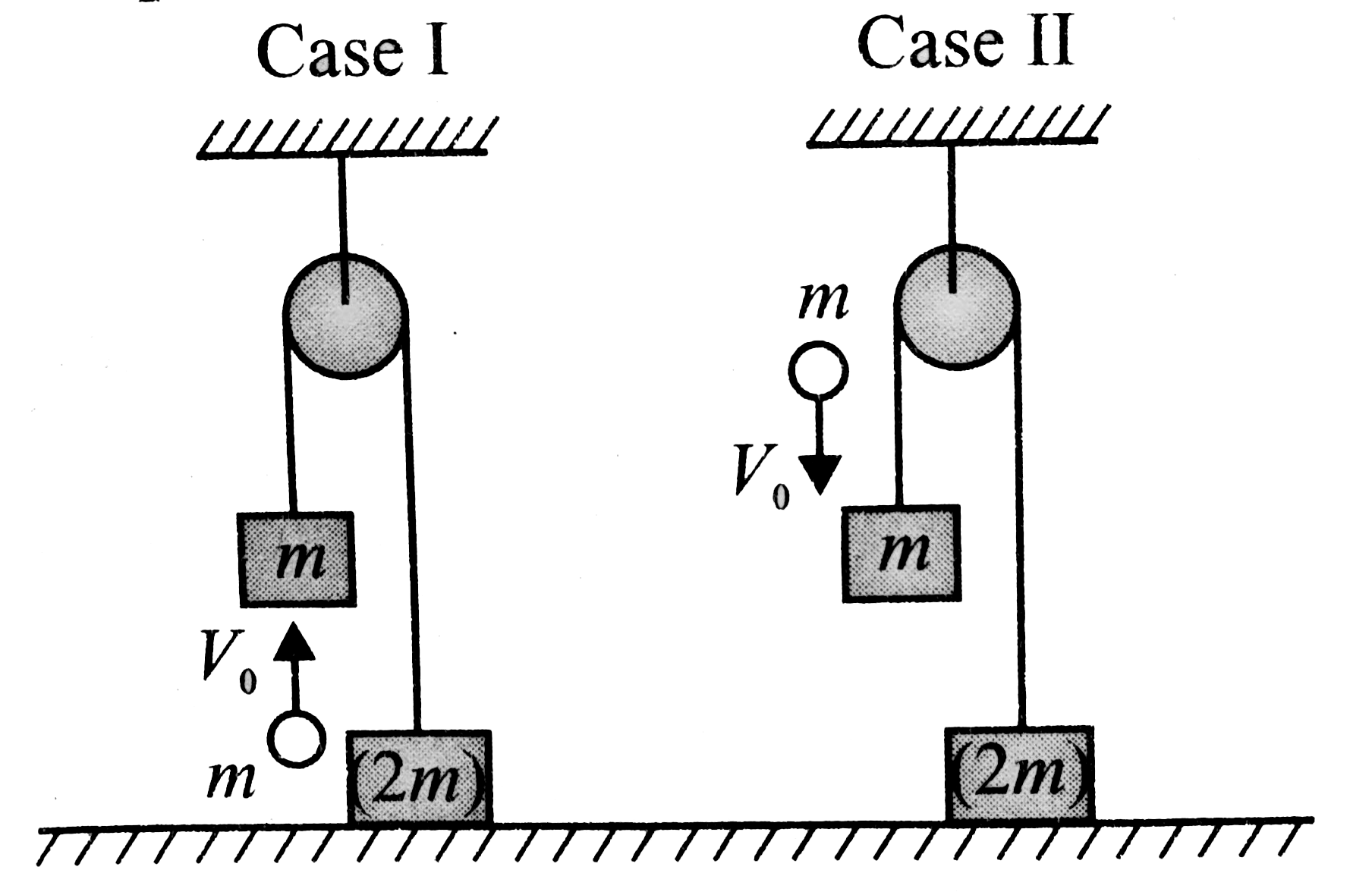
Two masses 2m and m are connected by an inextensible light string. The string is passing over a light frictionless pulley. The mass 2m is resting on a surface and mass m is hanging in air as shown in the figure. A particle of mass m strikes the mass m from below and with a velocity v0 and sticks to it. In another case a particle of mass m strikes the mass m with a velocity v) from top and sticks to it. Calculate the ratio of velocities of mass m just after collision in first and second case.
The correct Answer is:2
To solve the problem, we need to analyze the two cases of collisions separately and apply the principle of conservation of momentum.
2. Apply the conservation of momentum:
- Initial momentum before the collision = mv0
- Final momentum after the collision = (m+m)v′=2mv′
- Setting the initial momentum equal to the final momentum:
mv0=2mv′
3. Solve for v′:
- Dividing both sides by m:
v0=2v′
- Rearranging gives:
v′=v02
Case 2: Collision from Above
1. Identify the masses and velocities:
- Mass of the hanging block = m
- Mass of the particle striking from above = m
- Initial velocity of the particle = v0
- Let the velocity of the hanging mass after the collision be v′′.
2. Apply the conservation of momentum:
- Initial momentum before the collision = mv0
- Final momentum after the collision = mv′′+mv (where v is the velocity of the block after the collision)
- Setting the initial momentum equal to the final momentum:
mv0=mv′′+mv
3. Express the relationship:
- The tension in the string will affect the motion, but for simplicity, we can assume that the hanging mass m will have a downward acceleration due to gravity.
- Rearranging gives:
mv0=m(v′′+v)
- Since the hanging mass is not accelerating (it is in equilibrium), we can assume v=0 for the purpose of this calculation, leading to:
mv0=mv′′
4. Solve for v′′:
- Dividing both sides by m:
v0=v′′
Ratio of Velocities:
Now we have:
- Velocity after collision in Case 1: v′=v02
- Velocity after collision in Case 2: v′′=v04
To find the ratio of the velocities:
Ratio=v′v′′=v02v04=42=2
Final Answer:
The ratio of the velocities of mass m just after collision in the first and second case is 2.
- Initial momentum before the collision = mv0
- Final momentum after the collision = (m+m)v′=2mv′
- Setting the initial momentum equal to the final momentum:
mv0=2mv′
- Dividing both sides by m:
v0=2v′
- Rearranging gives:
v′=v02
1. Identify the masses and velocities:
- Mass of the hanging block = m
- Mass of the particle striking from above = m
- Initial velocity of the particle = v0
- Let the velocity of the hanging mass after the collision be v′′.
- Initial momentum before the collision = mv0
- Final momentum after the collision = mv′′+mv (where v is the velocity of the block after the collision)
- Setting the initial momentum equal to the final momentum:
mv0=mv′′+mv
- The tension in the string will affect the motion, but for simplicity, we can assume that the hanging mass m will have a downward acceleration due to gravity.
- Rearranging gives:
mv0=m(v′′+v)
- Since the hanging mass is not accelerating (it is in equilibrium), we can assume v=0 for the purpose of this calculation, leading to:
mv0=mv′′
- Dividing both sides by m:
v0=v′′
Now we have:
- Velocity after collision in Case 1: v′=v02
- Velocity after collision in Case 2: v′′=v04
Ratio=v′v′′=v02v04=42=2
The ratio of the velocities of mass m just after collision in the first and second case is 2.
Similar Questions
Two masses 2m and m are connected by an inextensible light string. The string is passing over a light frictionless pulley. The mass 2m is resting on a surface and mass in is hanging in air as shown in Fig. A particle of mass in strikes the mass in from below in case (I) with a velocity v0 and in case (II) strikes mass in with a velocity v0 from top and sticks to it.
 View Solution
View SolutionTwo blocks of masses m and M are connected by an inextensible light string . When a constant horizontal force acts on the block of mass M. The tension in the string is
 View Solution
View SolutionTwo masses m and M(m<M) are joined by a light string passing over a smooth and light pulley (as shown)
 View Solution
View SolutionTwo masses 2 kg and 4 kg are connected at two ends of light inextensible string passing over a frictionless pulley . If the masses are released , then find the accelaration of the masses and the tension in the string .
View SolutionTwo masses 2 kg and 4 kg are connected at the two ends of light inextensible string passing over a frictionless pulley. If the masses are released, then find the acceleration of the masses and the tension in the string.
View SolutionTwo masses m and M(>m) are joined by a light string passing over a smooth light pulley. The centre of mass of the system moves with an acceleration
 View Solution
View SolutionA particle of mass 2m moving with velocity v strikes a stationary particle of mass 3m and sticks to it . The speed of the system will be
View SolutionTwo particles of masses m and M(M>m) are connected by a cord that passes over a massless, frictionless pulley. The tension T in the string and the acceleration a of the particles is
View SolutionTwo bodies of masses m1 and m2(m1>m2) respectively are tied to the ends j of a string which passes over a light frictionless pulley. The masses are intitially at rest and released. What is the acceleration of the centre of mass ?
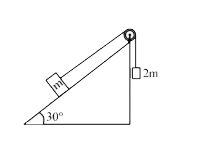
View SolutionTwo blocks of masses m and 2m are connected by a light string passing over a frictionless pulley. As shown in the figure, the mass m is placed on a smooth inclined plane of inclination 30° and 2m hangs vertically. If the system is released, the blocks move with an acceleration equal to :
 View Solution
View Solution
