The electric field intensity at all points in space is given by →E=√3ˆi−ˆj volts/metre. A square frame LMNO of side 1 metre is shown in figure. The point N lies in x-y plane. The initial angle between line ON and x-axis is θ=60∘
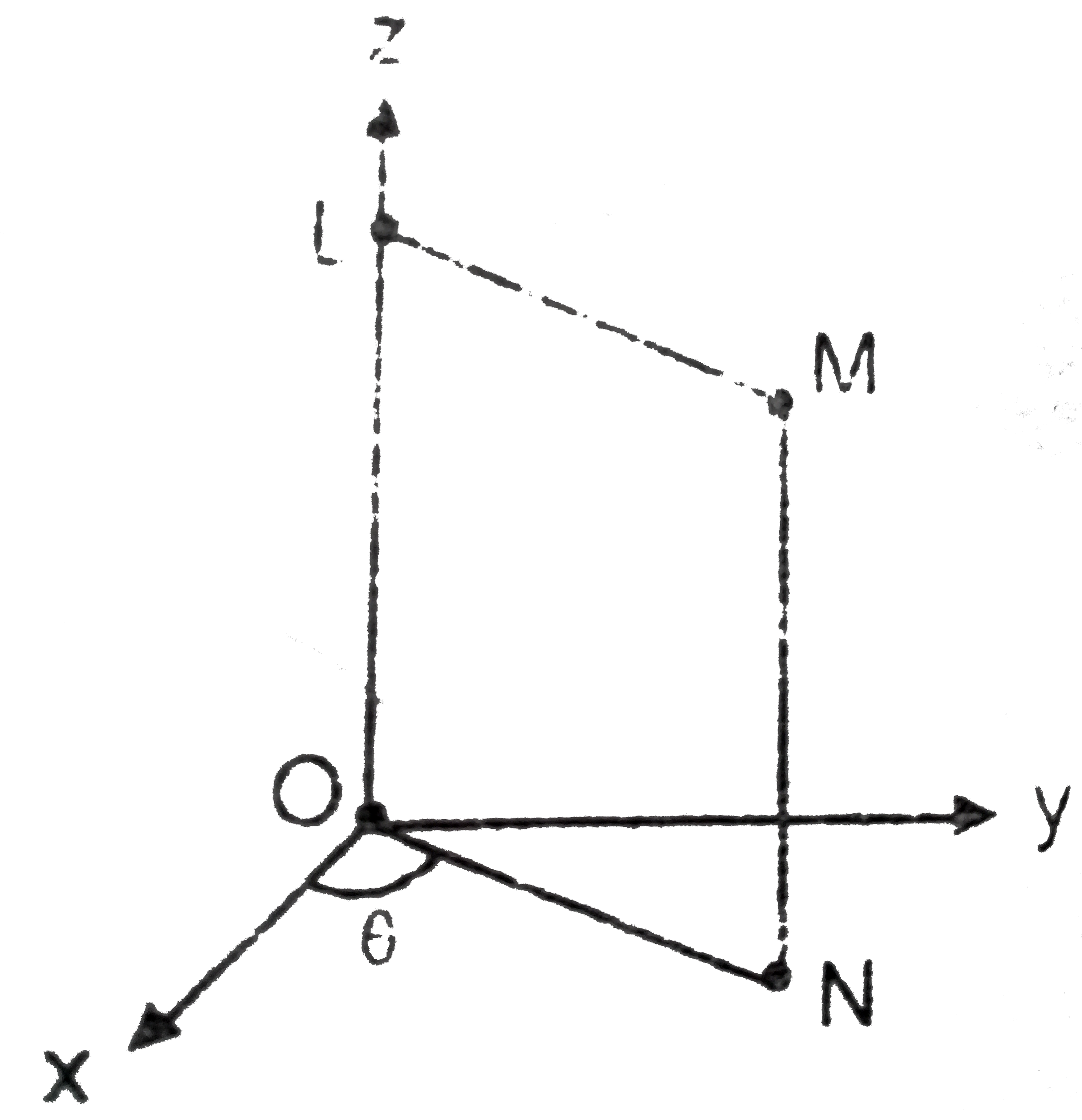
The magnitude of electric flux through area enclosed in square frame LMNO is -
0 V m
1 V m
2 V m
4 V m
The correct Answer is:C
Step by step video & image solution for The electric field intensity at all points in space is given by vec(E) = sqrt(3) hat (i) - hat (j) volts/metre. A square frame LMNO of side 1 metre is shown in figure. The point N lies in x-y plane. The initial angle between line ON and x-axis is theta = 60^(@) The magnitude of electric flux through area enclosed in square frame LMNO is - by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
the electric field intensity at all points is space is given by →E=√3ˆi−ˆj volts/meter. A square frame LMNO of side 1 meter is shown in the figure. The point N lies in x-y plane. The initial angle between line ON and x -axis is θ=60∘
the magnitude of electric flux through area enclosed in square frame LMNO is
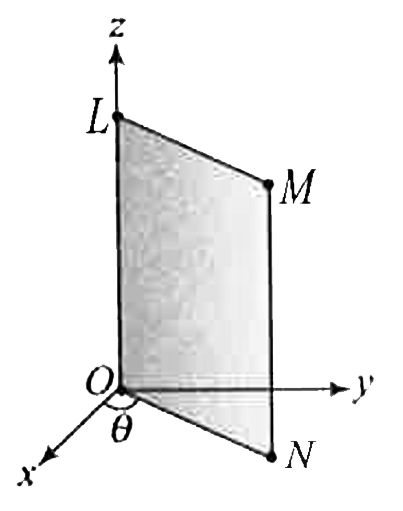
View SolutionThe electric field intensity at all points in space is given by →E=√3ˆi−ˆj volts/metre. A square frame LMNO of side 1 metre is shown in figure. The point N lies in x-y plane. The initial angle between line ON and x-axis is θ=60∘
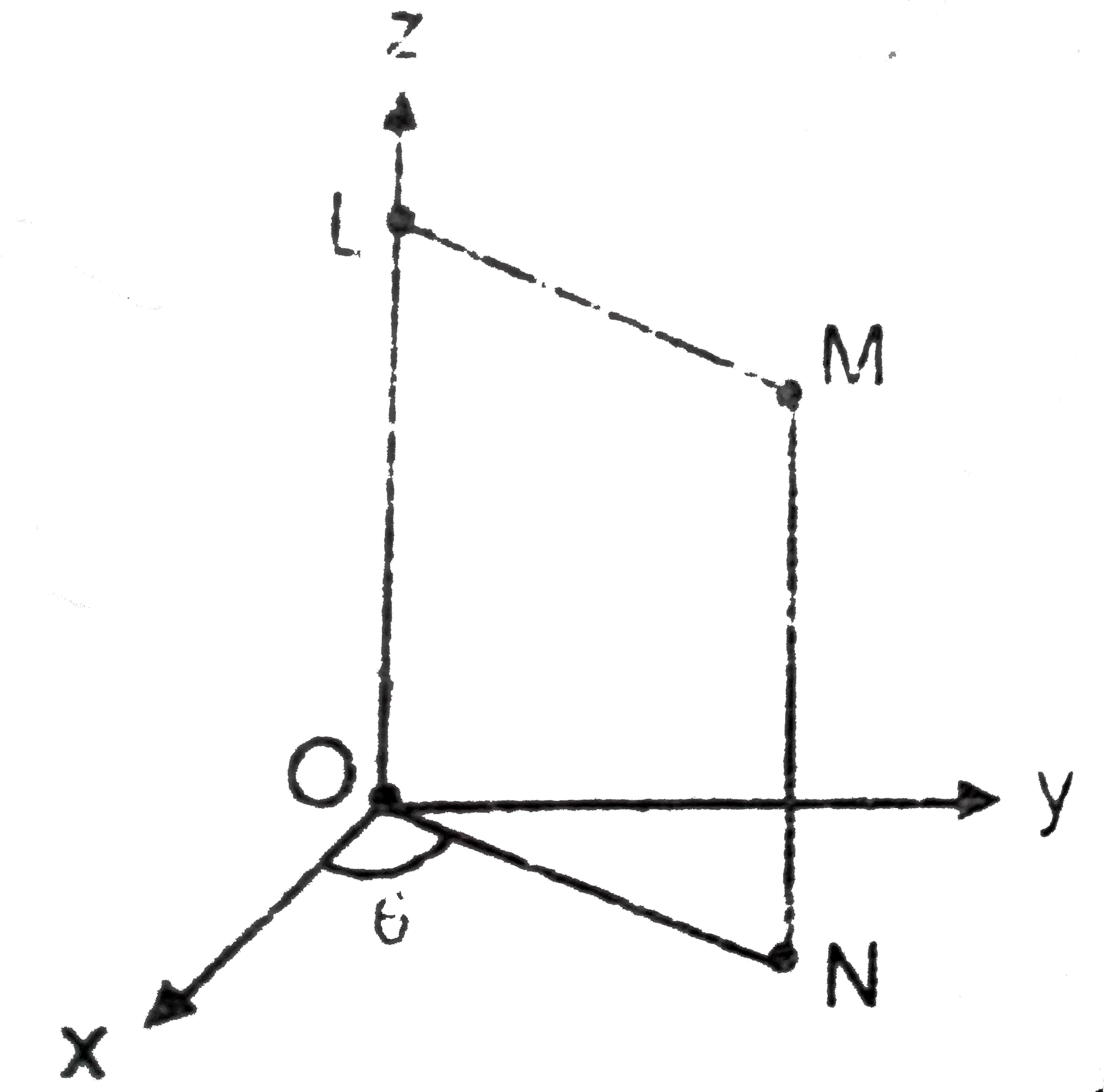
The work done by electric field in taking a point charge of 1μC from origin O to point M is -
View Solution
Knowledge Check
A square of side x m lies in the x-y plane in a region, when the magntic field is given by →B=B0(3ˆi+4ˆj+5ˆk) T, where B0 is constant. The magnitude of flux passing through the square is
A5B0x2WbB3B0x3WbC2B0x2WbDB0x2Wb
the electric field intensity at all points is space is given by →E=√3ˆi−ˆj volts/meter. A square frame LMNO of side 1 meter is shown in the figure. The point N lies in x-y plane. The initial angle between line ON and x -axis is θ=60∘
The work done by electric field in taking a point charge 1μC from origin O to point M is
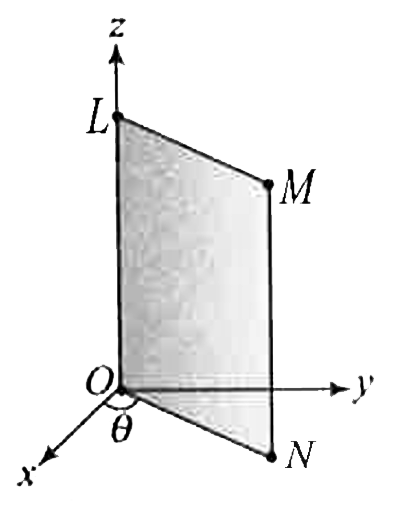
View SolutionThe electric field intensity at all points in space is given by →E=√3ˆi−ˆj V/m. The nature of equipotential lines is x-y plane is given by
View SolutionThe electric field in a region of space is given by, →E=E0ˆi+2E0ˆj where E0=100N/C. The flux of this field through a circular surface of radius 0.02m parallel to the Y-Z plane is nearly.
View SolutionA square of side L meters lies in the x-y plane in a region, where the magnetic field is given by B=B0(2ˆi+3ˆj+4ˆk)T, where B0 is constant. The magnitude of flux passing through the square is
View SolutionA square of side L meters lies in the x-y plane in a region, where the magnetic field is give by B=B0(2ˆi+3ˆj+4ˆk)T, where B0 is constant. The magnitude of flux passing through the square is
View SolutionA square of side L meters lies in the xy-plane in a region, where the magnetic field is given by =B0(2ˆi+3ˆj+4ˆk)T,, where B0 is constant. The magnitude of flux passing through the square is
View SolutionThe electric field in a region is given by E=aˆi+bˆj. Hence as and b are constants. Find the net flux passing through a square area of side I parallel to y-z plane.
View Solution
