The electric field intensity at all points in space is given by →E=√3ˆi−ˆj V/m. The nature of equipotential lines is x-y plane is given by


The correct Answer is:C
To solve the problem, we need to analyze the given electric field vector and determine the nature of the equipotential lines in the x-y plane.
1. Identify the Electric Field Vector:
The electric field intensity is given as:
→E=√3^i−^j(V/m)
Here, we can identify the components of the electric field:
- Ex=√3
- Ey=−1
2. Calculate the Angle of the Electric Field:
The angle θ that the electric field makes with the x-axis can be calculated using the tangent function:
θ=tan−1(EyEx)=tan−1(−1√3)
Evaluating this gives:
θ=−30∘
3. Determine the Angle of the Equipotential Lines:
Equipotential lines are always perpendicular to the electric field lines. Therefore, the angle ϕ that the equipotential lines make with the x-axis is given by:
ϕ=90∘+θ
Substituting the value of θ:
ϕ=90∘−30∘=60∘
4. Direction of Potential Change:
The electric field points in the direction of decreasing potential. Since Ex is positive and Ey is negative, the potential decreases in the positive x-direction and negative y-direction. This indicates that the equipotential lines will be oriented such that they decrease in potential towards the fourth quadrant.
5. Conclusion:
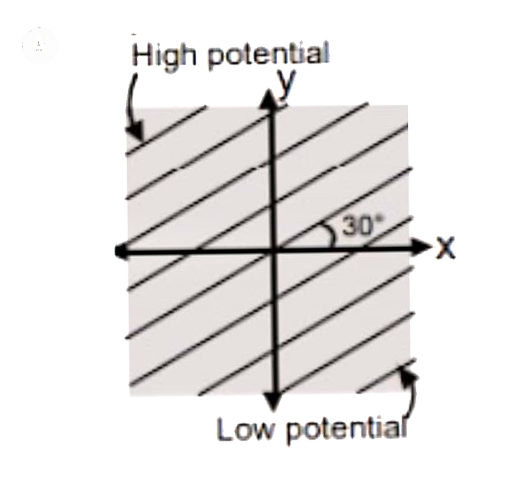
The equipotential lines will be straight lines making an angle of 60∘ with the x-axis, and they will be oriented such that the potential decreases towards the fourth quadrant.
Final Answer:
The nature of the equipotential lines in the x-y plane is that they are straight lines making an angle of 60∘ with the x-axis, decreasing in potential towards the fourth quadrant.
---
The electric field intensity is given as:
→E=√3^i−^j(V/m)
Here, we can identify the components of the electric field:
- Ex=√3
- Ey=−1
The angle θ that the electric field makes with the x-axis can be calculated using the tangent function:
θ=tan−1(EyEx)=tan−1(−1√3)
Evaluating this gives:
θ=−30∘
Equipotential lines are always perpendicular to the electric field lines. Therefore, the angle ϕ that the equipotential lines make with the x-axis is given by:
ϕ=90∘+θ
Substituting the value of θ:
ϕ=90∘−30∘=60∘
The electric field points in the direction of decreasing potential. Since Ex is positive and Ey is negative, the potential decreases in the positive x-direction and negative y-direction. This indicates that the equipotential lines will be oriented such that they decrease in potential towards the fourth quadrant.
The equipotential lines will be straight lines making an angle of 60∘ with the x-axis, and they will be oriented such that the potential decreases towards the fourth quadrant.
The nature of the equipotential lines in the x-y plane is that they are straight lines making an angle of 60∘ with the x-axis, decreasing in potential towards the fourth quadrant.
Similar Questions
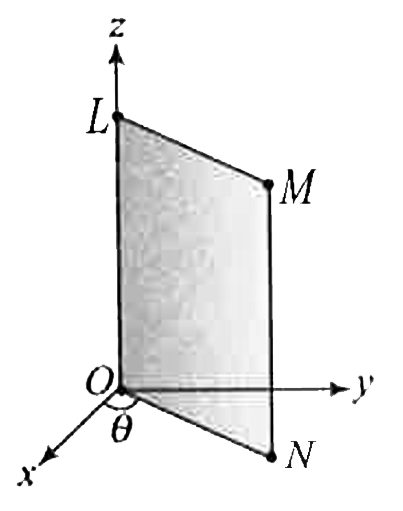
The electric field intensity at all points in space is given by →E=√3ˆi−ˆj volts/metre. A square frame LMNO of side 1 metre is shown in figure. The point N lies in x-y plane. The initial angle between line ON and x-axis is θ=60∘
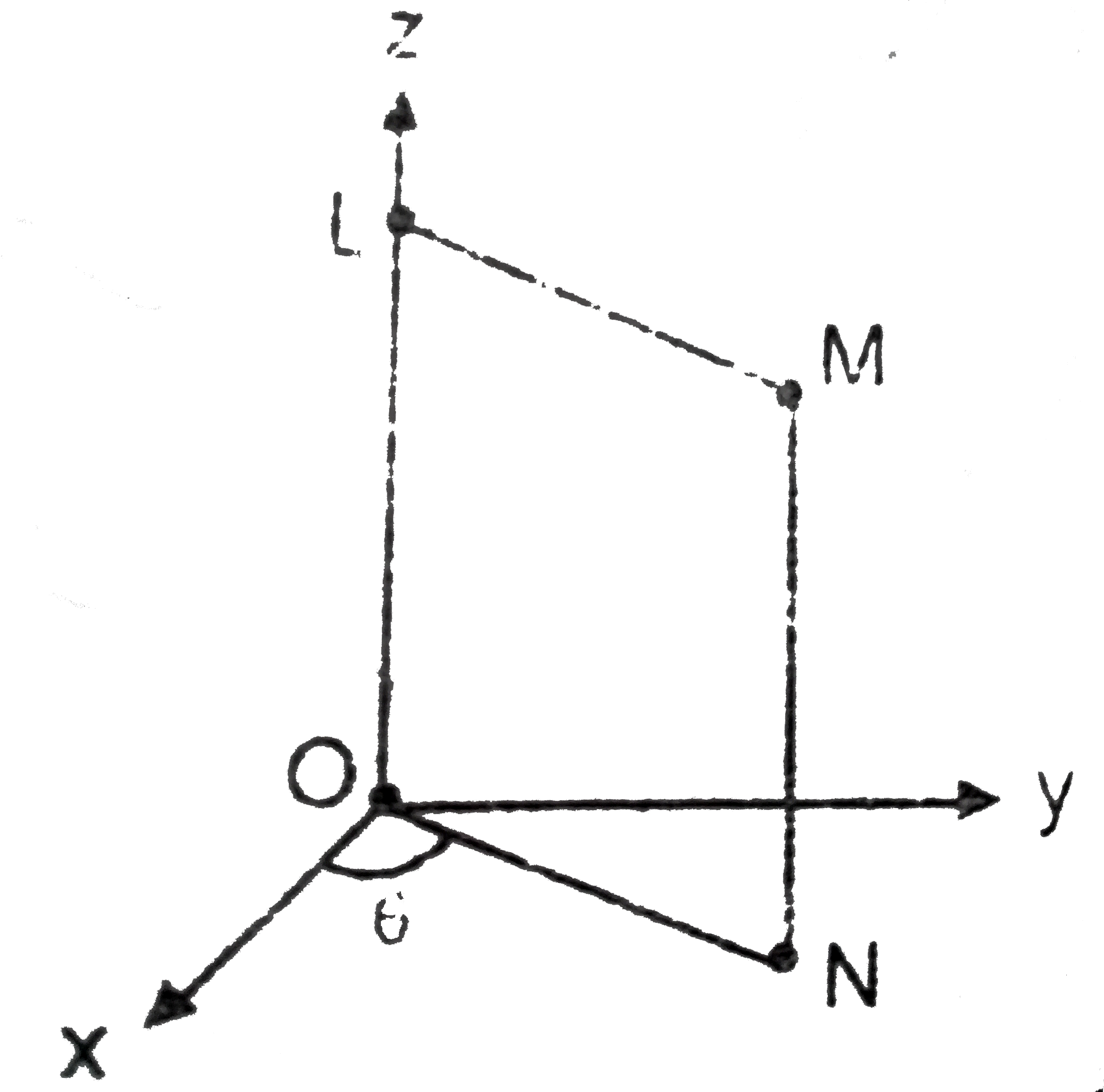
The work done by electric field in taking a point charge of 1μC from origin O to point M is -
View SolutionThe electric field intensity at all points in space is given by →E=√3ˆi−ˆj volts/metre. A square frame LMNO of side 1 metre is shown in figure. The point N lies in x-y plane. The initial angle between line ON and x-axis is θ=60∘
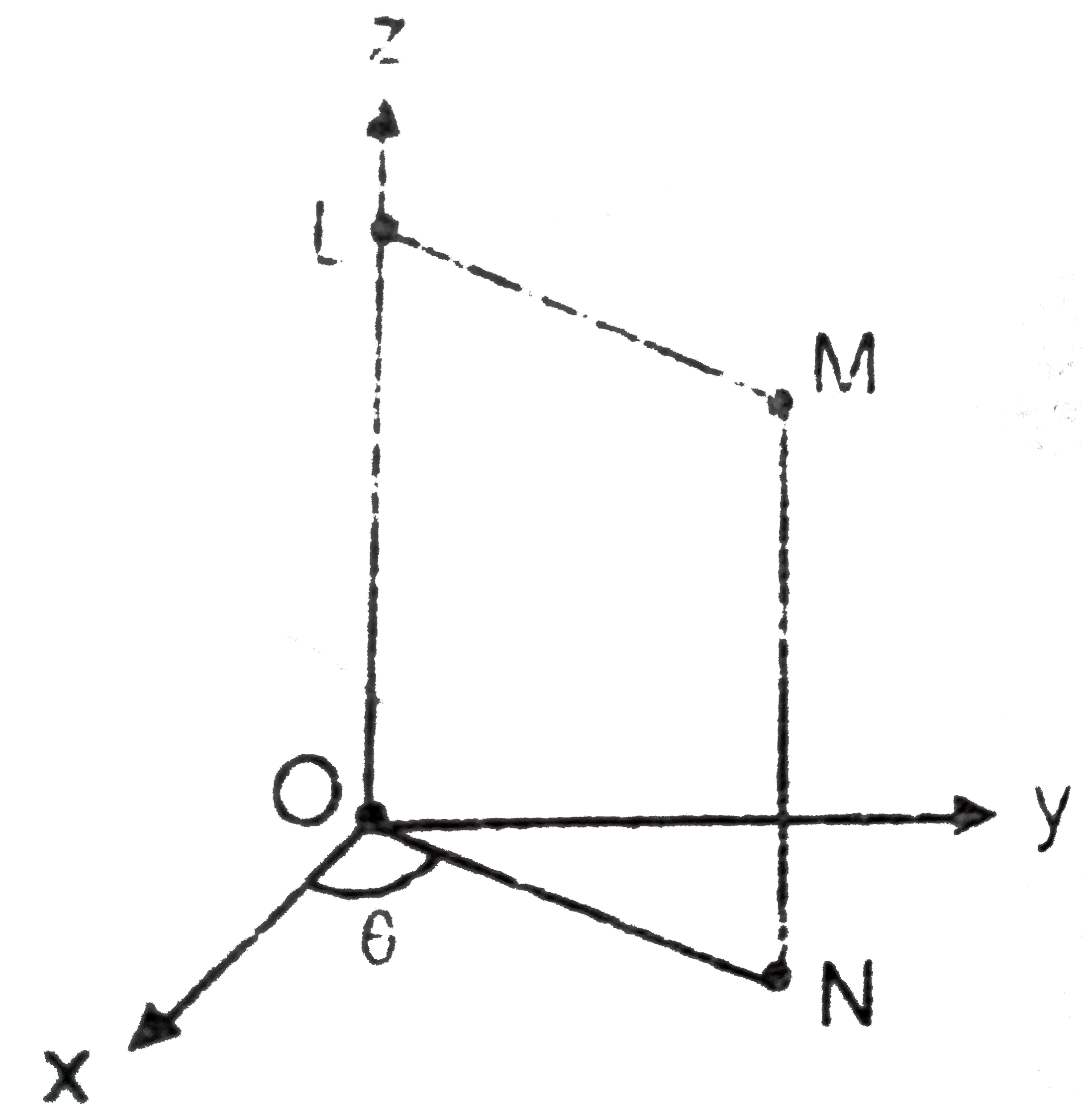
The magnitude of electric flux through area enclosed in square frame LMNO is -
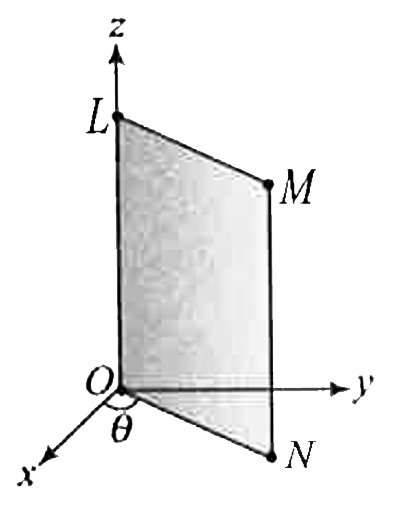
View Solutionthe electric field intensity at all points is space is given by →E=√3ˆi−ˆj volts/meter. A square frame LMNO of side 1 meter is shown in the figure. The point N lies in x-y plane. The initial angle between line ON and x -axis is θ=60∘
The work done by electric field in taking a point charge 1μC from origin O to point M is
View Solutionthe electric field intensity at all points is space is given by →E=√3ˆi−ˆj volts/meter. A square frame LMNO of side 1 meter is shown in the figure. The point N lies in x-y plane. The initial angle between line ON and x -axis is θ=60∘
the magnitude of electric flux through area enclosed in square frame LMNO is
View SolutionThe electrostatic potential V at any point (x, y, z) in space is given by V=4x2
View SolutionThe gravitational field in a region is given by →E=(yˆi+xˆj) N/kg, where x and y are in metres. The equipotential lines are plotted as
View SolutionThe electric field in a region of space is given by E=5ˆi+2ˆjN/C. The flux of E due ot this field through an area 1m2lying in the y-z plane, in SI units is
View SolutionThe electric field in a region is given by →E=(Ax3)ˆi. Write a suitable SI unit for A. Write an expression for the potential in the region assuming the potential at infinity to be zero.
View SolutionThe electric field in a certain region is given by E=(5ˆi−3ˆj)kV/m. Find the difference in potential VB−VA. If A is at the origin and point B is at a. (0,0,5)m, b. (4,0,3) m.
View SolutionElectrostatic field in a region is given by , vecE= (yzhati + zxhatj + xyhatk)V/m , where x,y and z are in m. If electric potential at origin is zero, then potential at (1m,1m, 1m) is
View Solution
