A thin non conducting disc of mass M = 2 kg, charge Q=2×102−C and radius R=16m is placed on a frictionless horizontal plane with its centre at the origin of the coordinate system. A non- uniform, radial magnetic field →B=B0ˆr is exists in space, where B0=10T and ˆr is a unit vector in the radially outward direction. The disc is set in motion with an angular velocity ω=x×102 rad s−1, about an axis passing through its centre and perpendicular to its plane, as shown in the figure. At what value of x, the disc will lift off from the surface.
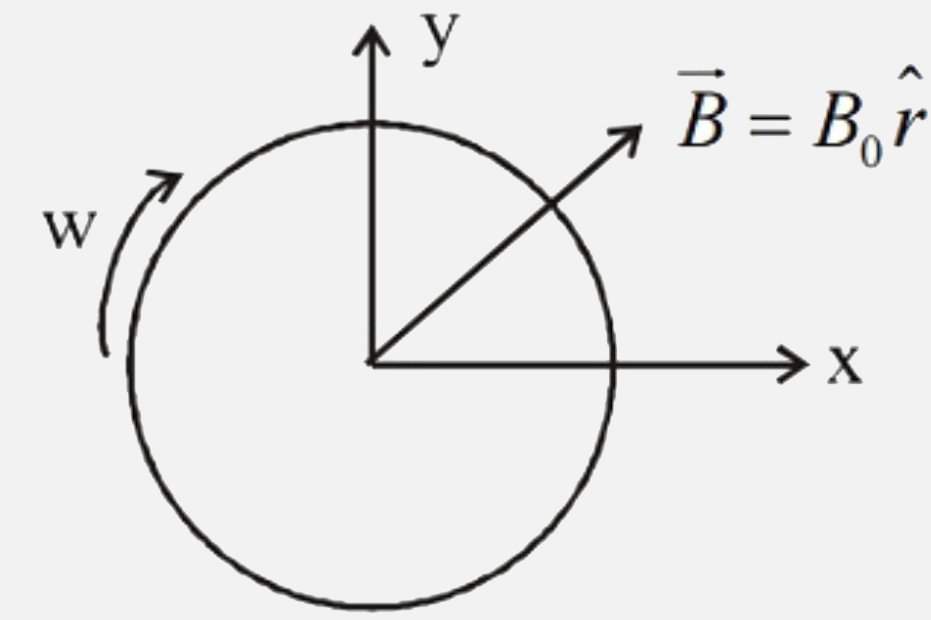
The correct Answer is:9
Step by step video & image solution for A thin non conducting disc of mass M = 2 kg, charge Q = 2 xx 10^(2-) C and radius R = (1)/(6)m is placed on a frictionless horizontal plane with its centre at the origin of the coordinate system. A non- uniform, radial magnetic field vecB = B_(0) hat(r) is exists in space, where B_(0)= 10 T and hat(r) is a unit vector in the radially outward direction. The disc is set in motion with an angular velocity omega = x xx 10^(2)" rad s"^(-1), about an axis passing through its centre and perpendicular to its plane, as shown in the figure. At what value of x, the disc will lift off from the surface. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
A rectangular loop of dimensions (a×b) carries a current i. A uniform magnetic field →B=B0ˆi exists in space. Then :
View SolutionA charge q is uniformly distributed on a non-conducting disc of radius R. It is rotated with an angular speed co about an axis passing through the centre of mass of the disc and perpendicular to its plane. Find the magnetic moment of the disc.
View SolutionAn electric field →E=Bxˆi exists in space, where B=20V/m2. Taking the potential at (2m, 4m) to be zero, find the potential at the origin.
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω . Another disc of same dimensions but of mass 14 M is placed gently on the first disc co-axially. The angular velocity of the system is
View SolutionA magnetic field →B=−B0ˆi exists within a sphere of radius R=v0T√3 where T is the time period of one revolution of a charged particle starting its motion form origin and moving with a velocity vce(v)0=v02√3ˆi−v02ˆj. Find the number of turns that the particle will take to come out of the magnetic field.
View SolutionA non - conducting ring of mass m = 4 kg and radius R = 10 cm has charge Q = 2 C uniformly distributed over its circumference. The ring is placed on a rough horizontal surface such that the plane of the ring is parallel to the surface. A vertical magnetic field B=4t3T is switched on at t = 0. At t = 5 s ring starts to rotate about the vertical axis through the centre. The coefficient of friction between the ring and the surface is found to be k24. Then the value of k is
View SolutionIn the space shown a non-uniform magnetic field →B=B0(1+x)(−ˆk) tesla is present. A closed loop of small resistance, placed in the xy plane is given velocity V0. The force due to magnetic field on the loop is
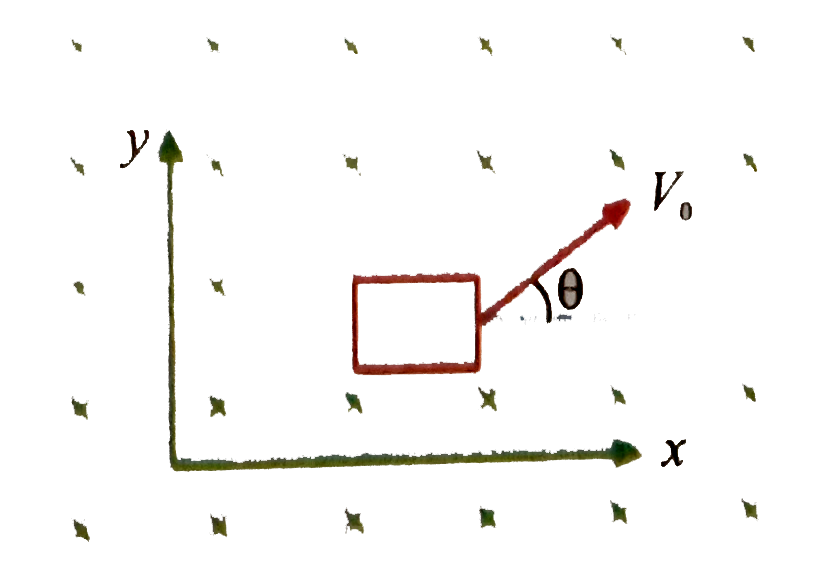
View SolutionIn the space shown a non-uniform magnetic field →B=B0(1+x)(−ˆk) tesla is present. A closed loop of small resistance, placed in the xy plane is given velocity V0. The force due to magnetic field on the loop is

View SolutionA uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then
Time (in second) at which ring start toppling is
View SolutionA uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then

Time (in second) at which ring start toppling is
View Solution
