A graph plotted between logt12 vs log concentration is a straight line. What is your conclusion?
[Given : n = order of reaction]
n=1,t12=1k.a
n=2,t12=1a
n=1,t12=0.693k
n=0,t12=a2k
The correct Answer is:C
To solve the problem, we need to analyze the relationship between the half-life of a reaction (t₁/₂) and the concentration of the reactants for different orders of reactions. The question states that a graph of log t₁/₂ versus log concentration is a straight line. Let's derive the conclusion step by step.
Step 1: Understanding the relationship for different orders of reactions
For different orders of reactions, the half-life (t₁/₂) is expressed in terms of the initial concentration ((A)) and the rate constant (k) as follows:
1. Zero-order reaction:
t1/2=(A)02k
2. First-order reaction:
t1/2=0.693k
3. Second-order reaction:
t1/2=1k(A)0
Step 2: Analyzing the zero-order reaction
For a zero-order reaction, we can express the half-life in terms of the initial concentration:
t1/2=(A)02k
Taking logarithms on both sides:
logt1/2=log((A)02k)=log(A)0−log(2k)
This shows that:
logt1/2=log(A)0−log(2k)
This equation indicates that if we plot log t₁/₂ against log (A), we will get a straight line with a slope of 1 and a y-intercept of −log(2k).
Step 3: Analyzing the first-order reaction
For a first-order reaction, the half-life is constant and does not depend on the concentration:
t1/2=0.693k
Taking logarithms:
logt1/2=log(0.693)−log(k)
This indicates that the plot of log t₁/₂ versus log (A) will not yield a straight line, as the half-life is independent of concentration.
Step 4: Analyzing the second-order reaction
For a second-order reaction:
t1/2=1k(A)0
Taking logarithms:
logt1/2=log(1k)−log(A)0
This also indicates that the plot will not yield a straight line, as the relationship is not linear.
Conclusion
Since the graph of log t₁/₂ versus log concentration is a straight line, we can conclude that the reaction is of zero order. The relationship derived confirms that the half-life is directly proportional to the initial concentration, which is characteristic of zero-order kinetics.
Final Answer
The conclusion is that the order of the reaction is zero (n = 0), and the relationship is given by:
t1/2=(A)02k
For different orders of reactions, the half-life (t₁/₂) is expressed in terms of the initial concentration ((A)) and the rate constant (k) as follows:
t1/2=(A)02k
2. First-order reaction:
t1/2=0.693k
3. Second-order reaction:
t1/2=1k(A)0
For a zero-order reaction, we can express the half-life in terms of the initial concentration:
t1/2=(A)02k
Taking logarithms on both sides:
logt1/2=log((A)02k)=log(A)0−log(2k)
This shows that:
logt1/2=log(A)0−log(2k)
This equation indicates that if we plot log t₁/₂ against log (A), we will get a straight line with a slope of 1 and a y-intercept of −log(2k).
For a first-order reaction, the half-life is constant and does not depend on the concentration:
t1/2=0.693k
Taking logarithms:
logt1/2=log(0.693)−log(k)
This indicates that the plot of log t₁/₂ versus log (A) will not yield a straight line, as the half-life is independent of concentration.
For a second-order reaction:
t1/2=1k(A)0
Taking logarithms:
logt1/2=log(1k)−log(A)0
This also indicates that the plot will not yield a straight line, as the relationship is not linear.
Since the graph of log t₁/₂ versus log concentration is a straight line, we can conclude that the reaction is of zero order. The relationship derived confirms that the half-life is directly proportional to the initial concentration, which is characteristic of zero-order kinetics.
The conclusion is that the order of the reaction is zero (n = 0), and the relationship is given by:
t1/2=(A)02k
Similar Questions
A graph plotted between log t50% vs log concentration is a straight line. What conclusion can you draw from this graph?
View SolutionFor a lst order reaction , a straight line is obtained if you plot
View SolutionFollowing is the graph between logt1/2 and loga (a initial concentration) for a given reaction at 300K

Find the order of reaction.
View SolutionA graph plotted between logk versus 1/T for calculating activation energy is shown by
View SolutionA graph between logt12 and log a (abscissa), a being the initial concentration of A in the reaction For reaction A→Product, the rate law is :
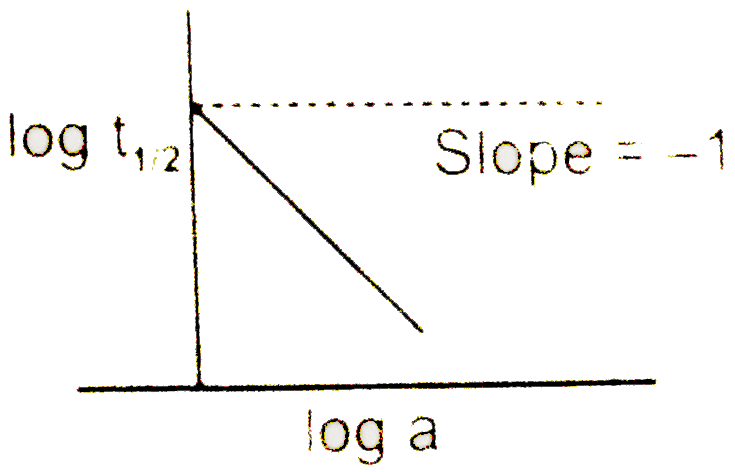
View SolutionA graph between logt12 and log a (abscissa), a being the initial concentration of A in the reaction For reaction A→Product, the rate law is :

View SolutionThe graph between logk versus 1/T is a straight line.
View SolutionIf t1/2vs1a2 is a straight line graph then determine the order of reaction.
View SolutionAt constant temperature if a graph plotted between logP and log(1V) has an intercept of unity then what will be the value of constant (k)
View SolutionConsider the following reaction
A→P1,B→P2,C→P3,D→P4,
The order of the above reaction are a,b,c and d, respectively . The following graph is obtained when log [rate ] vs. log [conc.] are plotted :
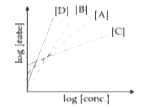
Among the following the correct sequence for the order of the reaction is :
View Solution
