If t1/2vs1a2 is a straight line graph then determine the order of reaction.
Zero order
First order
Second order
Third order
To determine the order of the reaction based on the relationship between half-life (t₁/₂) and the concentration (1/a²), we can follow these steps:
1. Understanding the Relationship:
We know that for an nth order reaction, the half-life (t₁/₂) is related to the concentration (a) of the reactant. The general formula for the half-life of an nth order reaction is:
t1/2∝1an−1
2. Given Information:
The problem states that the graph of t₁/₂ versus (1/a²) is a straight line. This implies that we can express the relationship as:
t1/2=k⋅1a2
where k is a constant.
3. Comparing the Equations:
From the general relationship, we have:
t1/2∝1an−1
and from the given information, we have:
t1/2∝1a2
By comparing the two proportionalities, we can set:
n−1=2
4. Solving for n:
Rearranging the equation gives us:
n=2+1=3
5. Conclusion:
Therefore, the order of the reaction is 3.
Final Answer:
The order of the reaction is 3.
---
We know that for an nth order reaction, the half-life (t₁/₂) is related to the concentration (a) of the reactant. The general formula for the half-life of an nth order reaction is:
t1/2∝1an−1
The problem states that the graph of t₁/₂ versus (1/a²) is a straight line. This implies that we can express the relationship as:
t1/2=k⋅1a2
where k is a constant.
From the general relationship, we have:
t1/2∝1an−1
and from the given information, we have:
t1/2∝1a2
By comparing the two proportionalities, we can set:
n−1=2
Rearranging the equation gives us:
n=2+1=3
Therefore, the order of the reaction is 3.
The order of the reaction is 3.
Similar Questions
For the reaction A→products , the graph of the fraction of A remaining as a function of time (x− axis ) is a straight line with −ve slpe . The order of the reaction is therefore
View SolutionIn the reaction A+B→C+D, the rate (dxdt) when plotted against time 't' gives a straight line parallel to time aixs.
The order and rate of reaction will be:
View SolutionThe variation of lnKc vs. lT gives straight line having an angle of 45∘ . The value of heat of reaction in Cal is _____
View SolutionA graph plotted between logt12 vs log concentration is a straight line. What is your conclusion?
[Given : n = order of reaction]
View SolutionFollowing is the graph between logt1/2 and loga (a initial concentration) for a given reaction at 300K

Find the order of reaction.
View SolutionWhat is the ratio of t1/2 to t1/3 (for the amount of substance left) for first order reaction ?
View SolutionA particle move with velocity v1 for time t1andv2 for time t2 along a straight line. The magntidue of its average acceleration is
View SolutionThe plot of concentration of the reactant vs time for a reaction is a straight line with a negative slope. This reaction follows
(a)zero order rate equation
(b)first order rate equation
(c)second order rate equation
(d)third order rate equation
View SolutionA graph between logt12 and log a (abscissa), a being the initial concentration of A in the reaction For reaction A→Product, the rate law is :
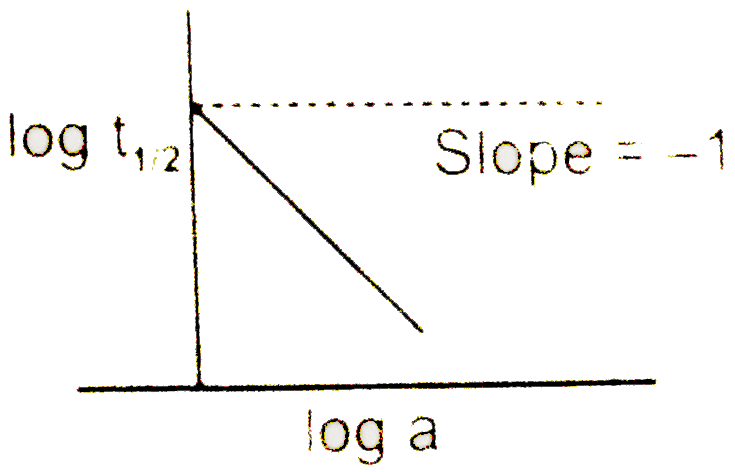
View SolutionA graph between logt12 and log a (abscissa), a being the initial concentration of A in the reaction For reaction A→Product, the rate law is :

View Solution
