If from the top of a tower, 60 meters high, the angles of depression of the top an floor of a house are 30∘and60∘ respectively, then the height (in meters) of the house is
The correct Answer is:40
To solve the problem step by step, we will use trigonometric ratios and the properties of angles of depression.
1. Understand the Problem:
- We have a tower that is 60 meters high.
- The angles of depression to the top and the floor of a house are 30° and 60°, respectively.
- We need to find the height of the house.
2. Draw a Diagram:
- Draw a vertical line representing the tower (60 meters).
- Mark the top of the tower as point A and the bottom as point B.
- Draw a horizontal line from point A to represent the line of sight to the top of the house (point C) and another line to the bottom of the house (point D).
- The angle of depression to point C (top of the house) is 30°, and to point D (floor of the house) is 60°.
3. Identify Angles:
- The angle of depression from A to C is 30°, which means the angle at point A (between the horizontal line and the line AC) is also 30°.
- The angle of depression from A to D is 60°, which means the angle at point A (between the horizontal line and the line AD) is also 60°.
4. Set Up the Right Triangles:
- For triangle ABC (top of the house):
- Let the horizontal distance from the tower to the house be x.
- The height from point B to point C is 60−H (where H is the height of the house).
- Using the tangent function:
tan(30°)=60−Hx
- We know that tan(30°)=1√3, so:
1√3=60−Hx(1)
- For triangle ABD (floor of the house):
- The height from point B to point D is 60 meters.
- Using the tangent function:
tan(60°)=60x
- We know that tan(60°)=√3, so:
√3=60x(2)
5. Solve for x:
- From equation (2):
x=60√3=20√3
6. Substitute x into Equation (1):
- Substitute x back into equation (1):
1√3=60−H20√3
- Cross-multiply:
20√3=√3(60−H)
- Simplifying gives:
20=60−H
- Rearranging gives:
H=60−20=40
7. Conclusion:
- The height of the house is H=40 meters.
Final Answer:
The height of the house is 40 meters.
- We have a tower that is 60 meters high.
- The angles of depression to the top and the floor of a house are 30° and 60°, respectively.
- We need to find the height of the house.
- Draw a vertical line representing the tower (60 meters).
- Mark the top of the tower as point A and the bottom as point B.
- Draw a horizontal line from point A to represent the line of sight to the top of the house (point C) and another line to the bottom of the house (point D).
- The angle of depression to point C (top of the house) is 30°, and to point D (floor of the house) is 60°.
- The angle of depression from A to C is 30°, which means the angle at point A (between the horizontal line and the line AC) is also 30°.
- The angle of depression from A to D is 60°, which means the angle at point A (between the horizontal line and the line AD) is also 60°.
- For triangle ABC (top of the house):
- Let the horizontal distance from the tower to the house be x.
- The height from point B to point C is 60−H (where H is the height of the house).
- Using the tangent function:
tan(30°)=60−Hx
- We know that tan(30°)=1√3, so:
1√3=60−Hx(1)
- The height from point B to point D is 60 meters.
- Using the tangent function:
tan(60°)=60x
- We know that tan(60°)=√3, so:
√3=60x(2)
- From equation (2):
x=60√3=20√3
- Substitute x back into equation (1):
1√3=60−H20√3
- Cross-multiply:
20√3=√3(60−H)
- Simplifying gives:
20=60−H
- Rearranging gives:
H=60−20=40
- The height of the house is H=40 meters.
The height of the house is 40 meters.
Similar Questions
If from the top of a tower 80 meters high the angles of depression of the top and bottom of a house are 30∘and45∘ respectively, then the height of the house is
View SolutionFrom te top of a tower , 60 meters high, the angles of depression of the top and bottom of a pole are αandβ respectively .Find the height of the pole.
View SolutionFrom the top of a hill h metres high the angles of depression of the top and the bottom of a pillar are α and β respectively. The height (in metres ) of the pillar is
View SolutionFrom the top of a 50 m high tower, the angles of depression of the top and bottom of a pole are observed to be 45o and 60o respectively. Find the height of the pole.
View SolutionFrom the top of a cliff, the angle of depression of the top and bottom of a tower are observed to be 45∘ and 60∘ respectively. If the height of the tower is 20 m.
Find :
(i) the height of the cliff
(ii) the distance between the cliff and the tower.
View SolutionFrom the top of a building 60m high the angles of depression of the top and the bottom of a tower are observed to be 30o and 60o . Find the height of the tower.
View SolutionIn the given figure, A from the top of a building AB = 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30∘and60∘ respectively. Find :
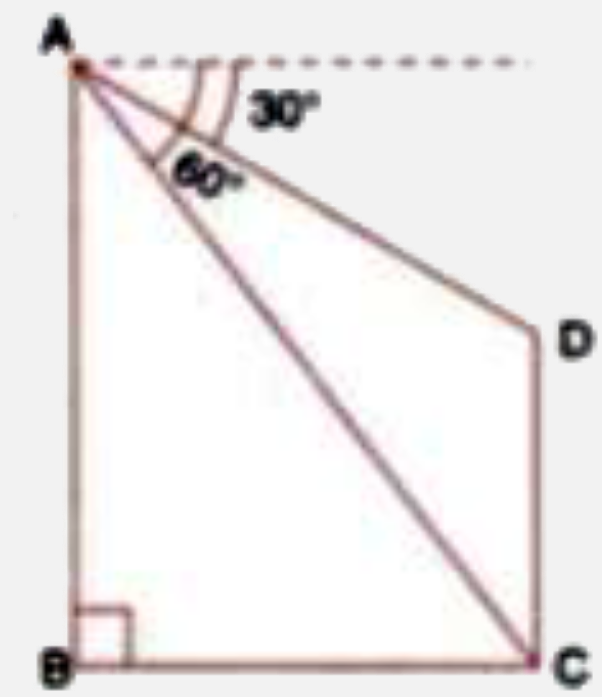
the horizontal distance between AB and CD
View SolutionFrom the top of a building AB , 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30o and 60o respectively. Find the height of the lamp post.
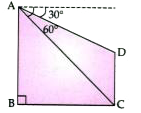
View SolutionIn the figure given, from the top of a building AB = 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30∘and60∘ respectively. Find :
(ii) the height of the lamp post.
View SolutionAt one side of a road, there os a house and on the other side there is a tower. House and tower are on the same horizontal plane. The angle of depression of the top and foot of the house, from the top of the tower are 30∘ and 45∘ respectively. If the height of the house is 10 m, then find the distance between the house and the tower.
View Solution
