A conductor with a cavity is charged positively and its surface charge density is σ. If E and V represent the electric field and potential, then inside the cavity
E = 0 and V = 0
E = 0 and σ- constant
V = 0 and σ = constant
E = 0 and V = constant
The correct Answer is:D
To solve the problem, we need to analyze the behavior of electric fields and potentials in and around a charged conductor with a cavity.
1. Understanding the Properties of Conductors:
- In electrostatic equilibrium, the electric field inside a conductor is zero. This is because free charges within the conductor rearrange themselves in response to electric fields until they cancel any internal fields.
2. Analyzing the Cavity:
- The cavity inside the conductor is a region where we need to determine the electric field (E) and the electric potential (V). Since the conductor is positively charged, the charges reside on the surface of the conductor.
3. Electric Field Inside the Cavity:
- Since the electric field inside a conductor is zero, and there are no charges present inside the cavity (the cavity is empty), the electric field inside the cavity must also be zero.
- Therefore, we conclude that:
E=0(inside the cavity)
4. Electric Potential Inside the Cavity:
- The electric potential inside the cavity can be understood by considering that the potential is constant throughout the cavity. This is because the electric field (E) is zero, which implies that there is no change in potential within that region.
- The potential inside the cavity (V) will be equal to the potential on the surface of the conductor, as the surface is where the charges are located.
- Thus, we have:
V=constant(inside the cavity)
5. Final Conclusion:
- The electric field inside the cavity is zero, and the potential is constant, equal to the potential on the surface of the conductor.
Summary:
- Electric Field (E) inside the cavity: E=0
- Electric Potential (V) inside the cavity: V=constant
- In electrostatic equilibrium, the electric field inside a conductor is zero. This is because free charges within the conductor rearrange themselves in response to electric fields until they cancel any internal fields.
- The cavity inside the conductor is a region where we need to determine the electric field (E) and the electric potential (V). Since the conductor is positively charged, the charges reside on the surface of the conductor.
- Since the electric field inside a conductor is zero, and there are no charges present inside the cavity (the cavity is empty), the electric field inside the cavity must also be zero.
- Therefore, we conclude that:
E=0(inside the cavity)
- The electric potential inside the cavity can be understood by considering that the potential is constant throughout the cavity. This is because the electric field (E) is zero, which implies that there is no change in potential within that region.
- The potential inside the cavity (V) will be equal to the potential on the surface of the conductor, as the surface is where the charges are located.
- Thus, we have:
V=constant(inside the cavity)
- The electric field inside the cavity is zero, and the potential is constant, equal to the potential on the surface of the conductor.
- Electric Field (E) inside the cavity: E=0
- Electric Potential (V) inside the cavity: V=constant
Similar Questions
A nonconducting sphere with a cavity has volume charge density ρ. O1andO2 represent the two centres as shown. The electric fields inside the cavity is E0. Now, an equal and opposite charge is given uniformly to the sphere on its outer surface. The magnitude of electric field inside the cavity becomes

View SolutionA spherical charged conductor has surface charge density σ.The intensity of electric field and potential on its surface are E and V .Now radius of sphere is halved keeping the charge density as constant .The new electric field on the surface and potential at the centre of the sphere are
View SolutionFigure shown a charged conductor resting on an insulating stand. If at the point P the charge density is σ, the potential is V and the electric field strength is E, what are the values of these quantities at point Q ?

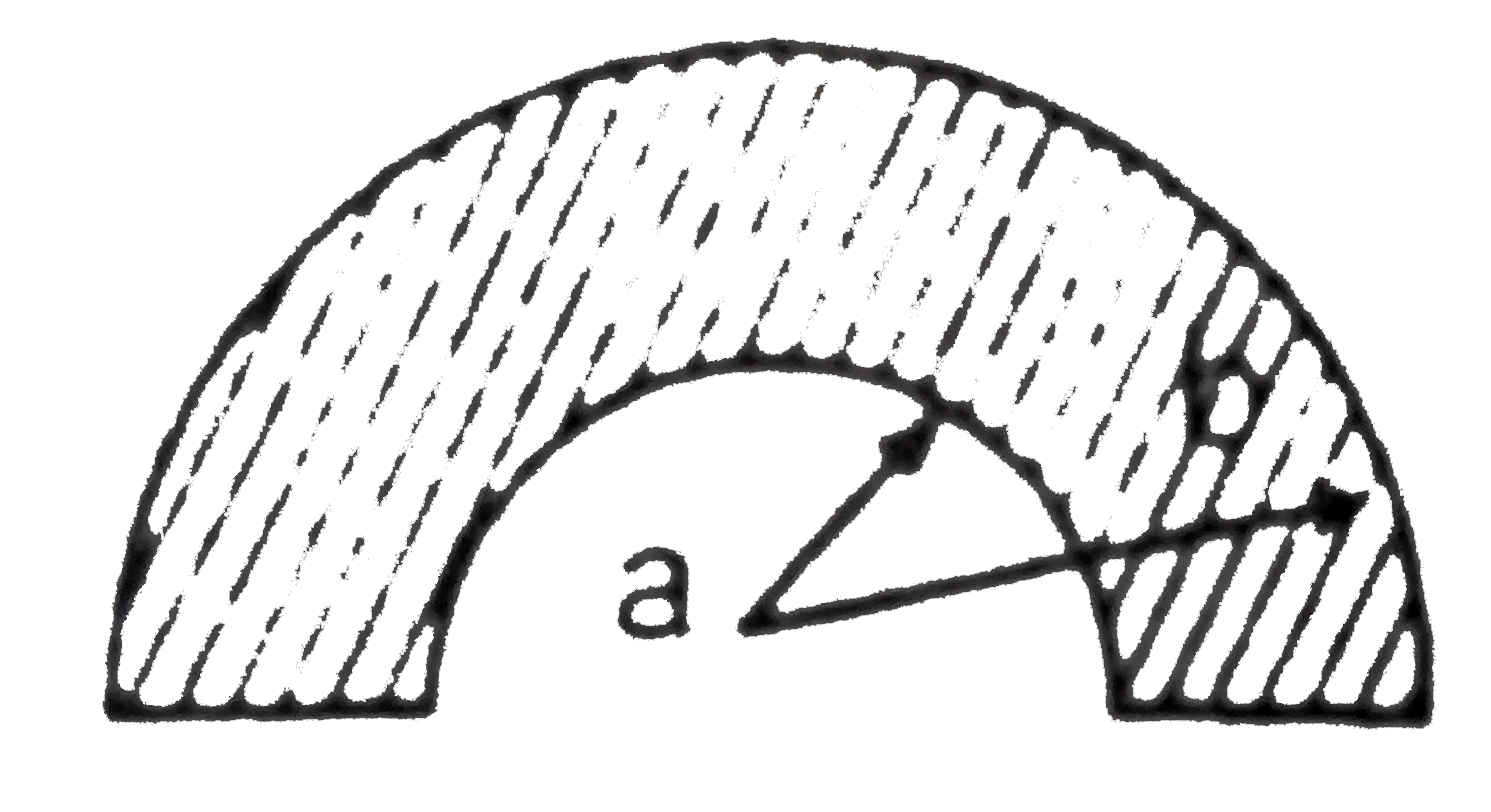
View SolutionA non-conducting semi circular disc (as shown in figure) has a uniform surface charge density σ. The ratio of electric field to electric potential at the centre of the disc will be
View SolutionThe electric field inside a spherical shell of uniform surface charge density is
View SolutionTwo concentric spheres of radii R and r have similar charges with equal surface charge densities (σ). The electric potential at their common centre is
View SolutionTwo thin infinite parallel plates have uniform charge densities +σ and −σ. The electric field in the space between them is
View SolutionA spherical charged conductor has surface charge density σ.The intensity of electric field and potential on its surface are E and V, now radius is halved keeping surface charge density to be constant. Then the new values will be
View SolutionA solid sphere of radius 'R' has a cavity of radius R2. The solid part has a uniform charge density 'ρ' and cavity has no charge. Find the electric potential at point 'A'. Also find the electric field (only magnetude) at point 'C' inside the cavity
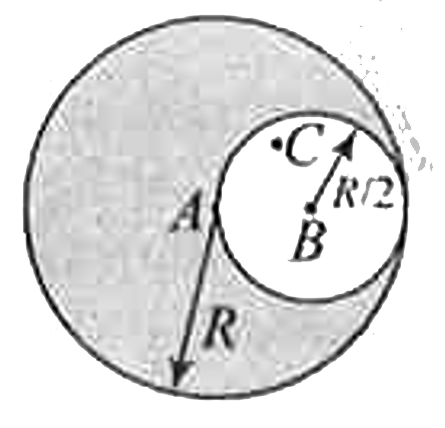
View SolutionAn infinite sheet of charge has surface charge density σ . The separation between two equipotential surfaces, whose potential differ by V is:
View Solution
