A body of mass m slides down an incline and reaches the bottom with a velocity v. If the same mass were in the form of a ring which rolls down this incline, the velocity of the ring at the bottom would have been
v
√2v
v√2
√25v
The correct Answer is:C
To solve the problem, we need to analyze the motion of both the sliding block and the rolling ring down the incline. Here's the step-by-step solution:
Step 1: Analyze the sliding block
1. When the block of mass m slides down the incline from a height H, it converts its potential energy into kinetic energy.
2. The potential energy (PE) at the top is given by:
\(
PE = mgh
\)
3. At the bottom, all this potential energy is converted into kinetic energy (KE), which is given by:
\(
KE = \frac{1}{2} mv^2
\)
4. Setting the potential energy equal to the kinetic energy:
\(
mgh = \frac{1}{2} mv^2
\)
5. Canceling m from both sides:
\(
gh = \frac{1}{2} v^2
\)
6. Rearranging gives:
\(
v^2 = 2gh
\)
7. Therefore, the velocity v of the block at the bottom is:
\(
v = \sqrt{2gh}
\)
This is our Equation 1.
Step 2: Analyze the rolling ring
1. When the ring rolls down the incline, it also has potential energy at the top:
\(
PE = mgh
\)
2. However, when it reaches the bottom, its energy is divided into translational kinetic energy and rotational kinetic energy:
\(
KE_{trans} = \frac{1}{2} mv_1^2
\)
\(
KE_{rot} = \frac{1}{2} I \omega^2
\)
3. For a ring, the moment of inertia I is given by:
\(
I = mr^2
\)
4. The relationship between linear velocity v1 and angular velocity ω is:
\(
v_1 = r\omega \quad \Rightarrow \quad \omega = \frac{v_1}{r}
\)
5. Substituting I and ω into the rotational kinetic energy:
\(
KE_{rot} = \frac{1}{2} (mr^2) \left(\frac{v_1}{r}\right)^2 = \frac{1}{2} mv_1^2
\)
6. Therefore, the total kinetic energy at the bottom is:
\(
KE_{total} = KE_{trans} + KE_{rot} = \frac{1}{2} mv_1^2 + \frac{1}{2} mv_1^2 = mv_1^2
\)
7. Setting the potential energy equal to the total kinetic energy:
\(
mgh = mv_1^2
\)
8. Canceling m from both sides:
\(
gh = v_1^2
\)
9. Rearranging gives:
\(
v_1^2 = gh
\)
10. Now, substituting the expression for h from Equation 1:
\(
h = \frac{v^2}{2g}
\)
11. Thus, we have:
\(
v_1^2 = g \left(\frac{v^2}{2g}\right) = \frac{v^2}{2}
\)
12. Therefore, the velocity v1 of the ring at the bottom is:
\(
v_1 = \frac{v}{\sqrt{2}}
\)
Final Result
The velocity of the ring at the bottom of the incline is:
\(
v_1 = \frac{v}{\sqrt{2}}
\)
1. When the block of mass m slides down the incline from a height H, it converts its potential energy into kinetic energy.
2. The potential energy (PE) at the top is given by:
\(
PE = mgh
\)
3. At the bottom, all this potential energy is converted into kinetic energy (KE), which is given by:
\(
KE = \frac{1}{2} mv^2
\)
4. Setting the potential energy equal to the kinetic energy:
\(
mgh = \frac{1}{2} mv^2
\)
5. Canceling m from both sides:
\(
gh = \frac{1}{2} v^2
\)
6. Rearranging gives:
\(
v^2 = 2gh
\)
7. Therefore, the velocity v of the block at the bottom is:
\(
v = \sqrt{2gh}
\)
This is our Equation 1.
1. When the ring rolls down the incline, it also has potential energy at the top:
\(
PE = mgh
\)
2. However, when it reaches the bottom, its energy is divided into translational kinetic energy and rotational kinetic energy:
\(
KE_{trans} = \frac{1}{2} mv_1^2
\)
\(
KE_{rot} = \frac{1}{2} I \omega^2
\)
3. For a ring, the moment of inertia I is given by:
\(
I = mr^2
\)
4. The relationship between linear velocity v1 and angular velocity ω is:
\(
v_1 = r\omega \quad \Rightarrow \quad \omega = \frac{v_1}{r}
\)
5. Substituting I and ω into the rotational kinetic energy:
\(
KE_{rot} = \frac{1}{2} (mr^2) \left(\frac{v_1}{r}\right)^2 = \frac{1}{2} mv_1^2
\)
6. Therefore, the total kinetic energy at the bottom is:
\(
KE_{total} = KE_{trans} + KE_{rot} = \frac{1}{2} mv_1^2 + \frac{1}{2} mv_1^2 = mv_1^2
\)
7. Setting the potential energy equal to the total kinetic energy:
\(
mgh = mv_1^2
\)
8. Canceling m from both sides:
\(
gh = v_1^2
\)
9. Rearranging gives:
\(
v_1^2 = gh
\)
10. Now, substituting the expression for h from Equation 1:
\(
h = \frac{v^2}{2g}
\)
11. Thus, we have:
\(
v_1^2 = g \left(\frac{v^2}{2g}\right) = \frac{v^2}{2}
\)
12. Therefore, the velocity v1 of the ring at the bottom is:
\(
v_1 = \frac{v}{\sqrt{2}}
\)
The velocity of the ring at the bottom of the incline is:
\(
v_1 = \frac{v}{\sqrt{2}}
\)
Similar Questions
A body of mass m slides down an smooth incline and reaches the bottom with a velocity, Now smooth incline surface is made rough and the same mass was in the form of a ring which rolls down this incline, the velocity of the ring at the bottom would have been:
View SolutionWhen a point mass slips down a smooth incline from top, it reaches the bottom with linear speed v. If same mass in the form of disc rolls down without slipping a rough incline of identical geometry through same distance, what will be its linear velocity at the bottom ?
View SolutionA body is released from the top of a smooth inclined plane of inclination θ. It reaches the bottom with velocity v. If the angle of inclina-tion is doubled for the same length of the plane, what will be the velocity of the body on reach ing the ground .
View SolutionA solid iron sphere A rolls down an inclined plane, while another hollow sphere B with the same mass and same radius also rolls down the inclided plane. If VA and VB are their velocities a the bottom of the inclined plane. Then
A. VA>VB
B. VA=VB
C. VA<VB
D. VA>=<VB
View SolutionIf a ring, a disc, a solid sphere and a cyclinder of same radius roll down an inclined plane, the first one to reach the bottom will be:
View SolutionA block is placed on the top of a plane inclined at 37∘ with horizontal. The length of the plane is 5m. The block slides down the plane and reaches the bottom.
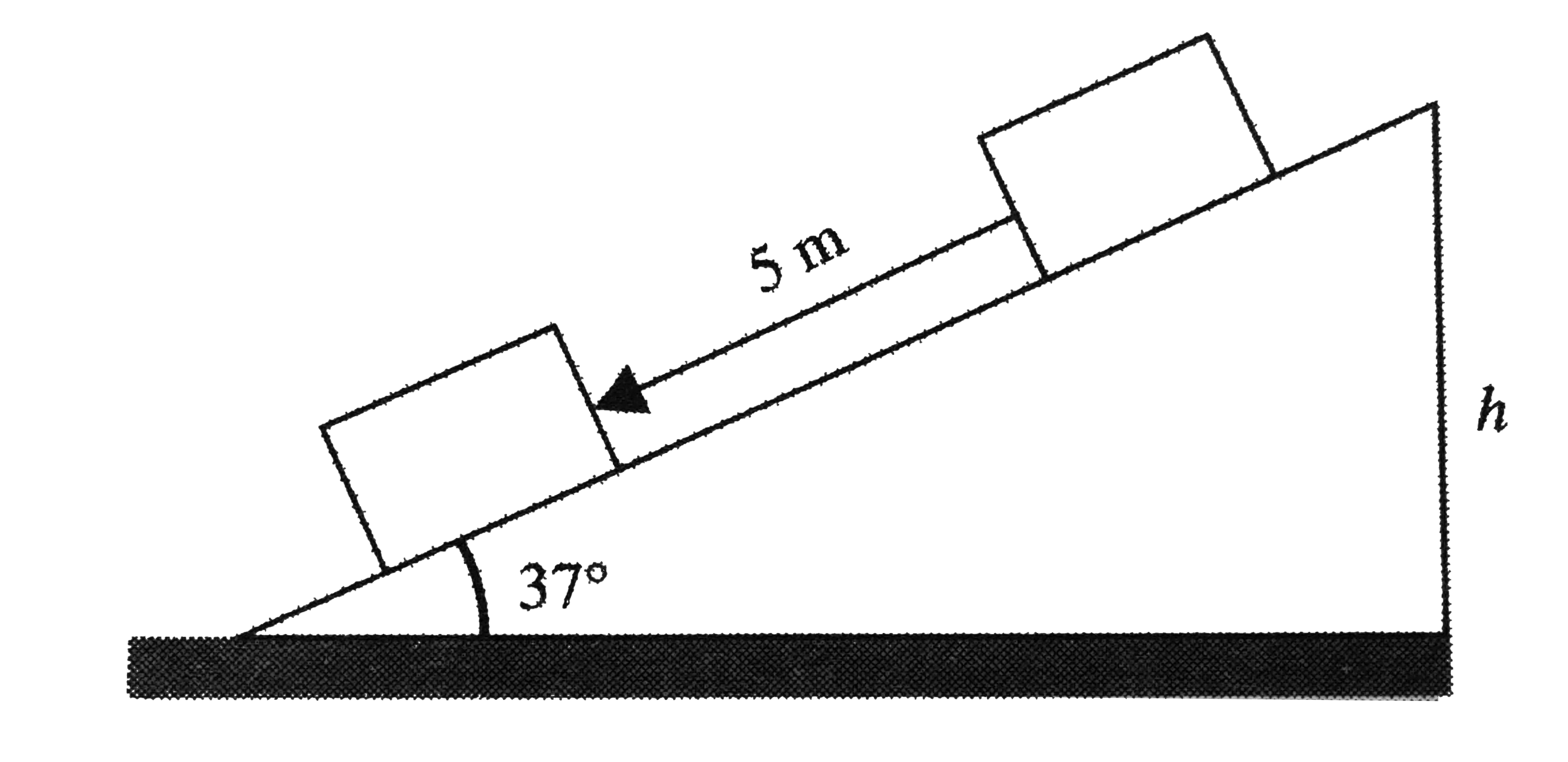
a. Find the speed of the block at the bottom if the inclined plane is smooth.
b. Find the speed of the block at the bottom if the coefficient of friction is 0.25.
View SolutionA block of mass m slides down along the surface of the bowl from the rim to the bottom as shown in fig. The velocity of the block at the bottom will be-

View SolutionA block moves down a smooth inclined plane of inclination θ. Its velocity on reaching the bottom is v. If it slides down a rough inclined plane of some inclination, its velocity on reaching the bottom is v/n, where n is a number greater than 0. The coefficient of friction is given by -
View SolutionA disc of mass 3 kg rolls down an inclined plane of height 5 m. The translational kinetic energy of the disc on reaching the bottom of the inclined plane is
View SolutionA small disc is released from rest at A on an inclined plane AB so that it rolls down without slipping. It reaches the bottom with linear velocity v1 in time t1. Next a small ring released form rest on the inclined plane AC so that it rolls down without slipping. It reaches the bottom with linear vlocity v2 in time t2. Given θ1=30∘,θ2=60∘, and h=10m. Then,
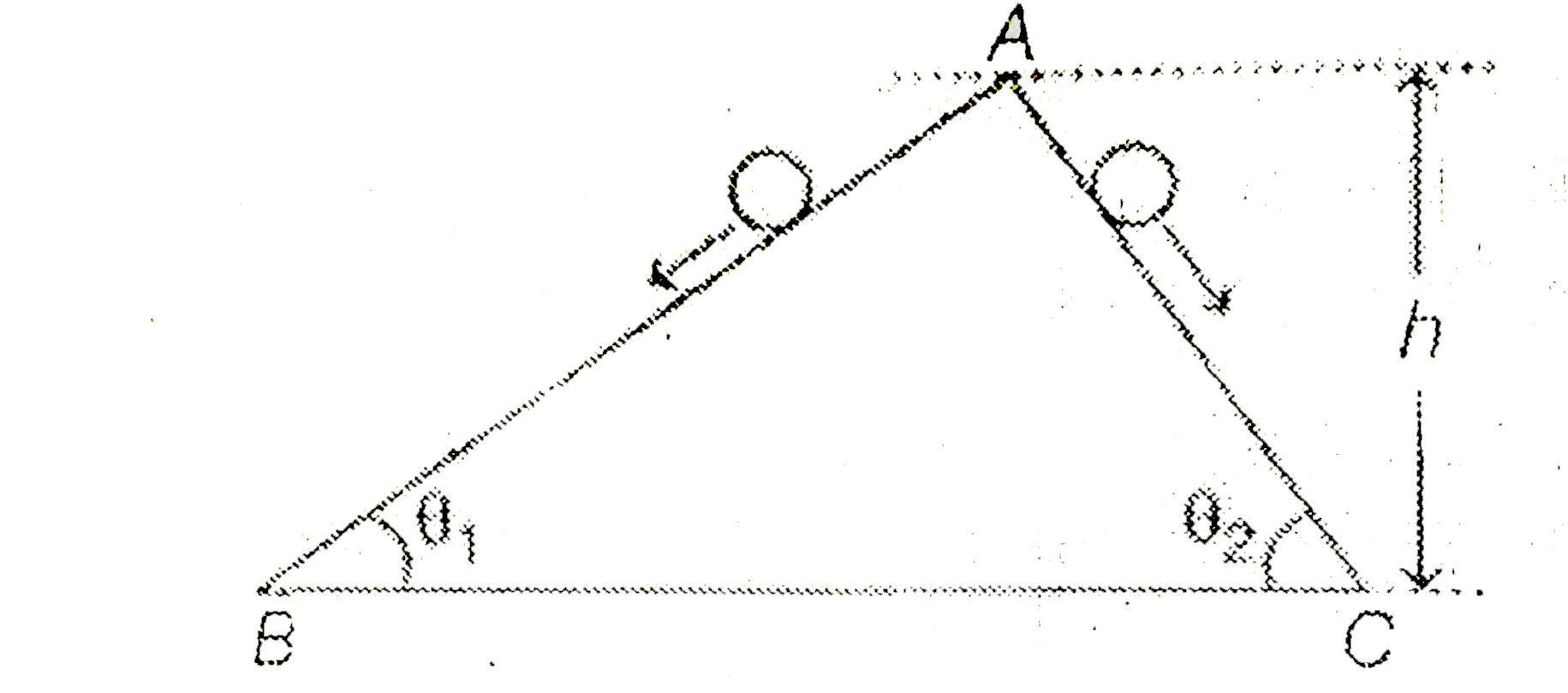
View Solution