Gravitational force acts on a particle due to fixed uniform solid sphere. Neglect other forces. Then particle
always moves normal to the radial direction.
always moves in the radial direction only.
always moves in circular orbit.
experiences a force directed along the radial direction only.
The correct Answer is:D
To solve the problem regarding the gravitational force acting on a particle due to a fixed uniform solid sphere, we can follow these steps:
1. Understanding the System:
- We have a fixed uniform solid sphere with a particle located outside the sphere. The gravitational force acts on the particle due to the mass of the sphere.
2. Identifying the Gravitational Force:
- The gravitational force Fg acting on the particle (mass m) due to the sphere (mass M) can be expressed using Newton's law of gravitation:
Fg=GMmr2
where G is the gravitational constant, M is the mass of the sphere, m is the mass of the particle, and r is the distance between the center of the sphere and the particle.
3. Direction of the Gravitational Force:
- The gravitational force acts radially inward, meaning it pulls the particle towards the center of the sphere. This is a crucial point because it determines the motion of the particle.
4. Analyzing the Motion of the Particle:
- If the particle has no initial velocity, it will simply accelerate towards the sphere due to the gravitational attraction. If it had an initial velocity, we would need to analyze the components of that velocity to determine the path.
5. Conclusion on Motion:
- Since the gravitational force is directed radially inward, if the particle has no initial tangential velocity, it will move directly towards the center of the sphere along the radial line. If it had a tangential component, it could move in a circular orbit, but this is not the case here.
6. Final Statement:
- The correct interpretation of the motion of the particle is that it experiences a force directed along the radial direction only, which confirms that the particle will move towards the center of the sphere.
Answer:
The particle experiences a force directed along the radial direction only.
- We have a fixed uniform solid sphere with a particle located outside the sphere. The gravitational force acts on the particle due to the mass of the sphere.
- The gravitational force Fg acting on the particle (mass m) due to the sphere (mass M) can be expressed using Newton's law of gravitation:
Fg=GMmr2
where G is the gravitational constant, M is the mass of the sphere, m is the mass of the particle, and r is the distance between the center of the sphere and the particle.
- The gravitational force acts radially inward, meaning it pulls the particle towards the center of the sphere. This is a crucial point because it determines the motion of the particle.
- If the particle has no initial velocity, it will simply accelerate towards the sphere due to the gravitational attraction. If it had an initial velocity, we would need to analyze the components of that velocity to determine the path.
- Since the gravitational force is directed radially inward, if the particle has no initial tangential velocity, it will move directly towards the center of the sphere along the radial line. If it had a tangential component, it could move in a circular orbit, but this is not the case here.
- The correct interpretation of the motion of the particle is that it experiences a force directed along the radial direction only, which confirms that the particle will move towards the center of the sphere.
The particle experiences a force directed along the radial direction only.
Similar Questions
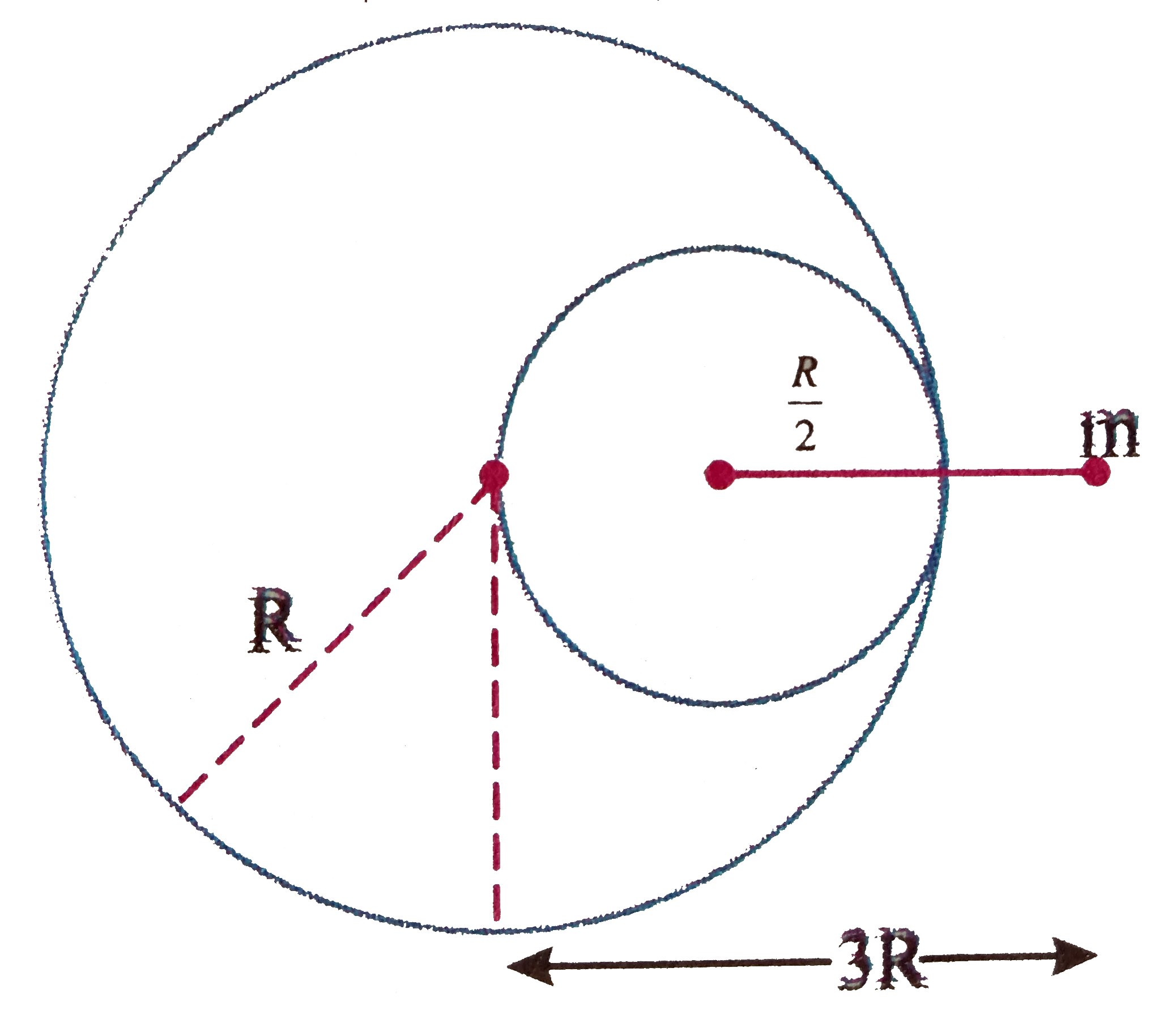
The gravitational force acting on a particle, due to a solid sphere of uniform density and radius R, at a distance of 3R from the centre of the sphere is F1. A spherical hole of radius (R/2) is now made in the sphere as shown in diagram. The sphere with hole now exerts a force F2 on the same particle. ratio of F1 to F2 is
View SolutionGravitational field due to a solid sphere
View Solution
Knowledge Check
Assertion: The gravitational force on a particle inside a spherical shell is zero.
Reason: The shell shields other bodies outside it form exerting gravitational forces on a particle inside.AIf both assertion and reason are true and reason is the correct explanation of assertionBIf both assertion and reason are truebut reason is not the correct explanation of assertionCIf assertion is true but reason is falseDIf both assertion and reason are false.
If a constant force acts on a particle, its acceleration will
View SolutionFour forces acting on a particle keep it in equilibrium, then :-
View SolutionThe gravitational force acting on a particle of 1 g due to a similar particle is equal to 6.67×10−17N. Calculate the separation between the particles.
View SolutionThe gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is
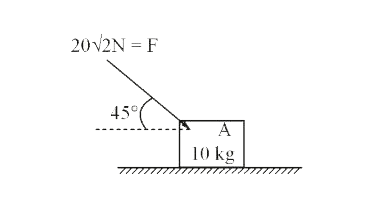
View SolutionA force F acts on a particle kept on a rough surface as shown in the figure. The particle is at rest. Find the net force applied by ground on the particle.
View SolutionThe momentum of a moving particle given by p=tlnt. Net force acting on this particle is defined by equation F=dpdt. The net force acting on the particle is zero at time
View SolutionThree particles, each of mass m are fixed at the vertices of an equilateral triangle of side length a. The only forces acting on the particles are their mutual gravitational forces. Then answer the following questions.
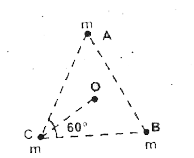
Force acting on particle C, due to particle A and B
View Solution
