If a constant force acts on a particle, its acceleration will
remain constant
gradually decrease
gradully increase
be undefined.
The correct Answer is:B
To solve the question, "If a constant force acts on a particle, its acceleration will," we can follow these steps:
Step 1: Understand the relationship between force, mass, and acceleration
According to Newton's second law of motion, the relationship between force (F), mass (m), and acceleration (a) is given by the equation:
F=m⋅a
This means that the force acting on an object is equal to the mass of the object multiplied by its acceleration.
Step 2: Analyze the given conditions
The problem states that a constant force is acting on the particle. This implies that the value of F is constant. Additionally, we need to consider the mass of the particle. If the velocity of the particle is much less than the speed of light (non-relativistic speeds), the mass of the particle can be considered constant.
Step 3: Determine the effect of constant force on acceleration
Since both the force (F) and mass (m) are constant (under non-relativistic conditions), we can rearrange the equation to find acceleration:
a=Fm
Since F is constant and m is constant, it follows that the acceleration (a) will also remain constant.
Step 4: Consider relativistic effects
However, if the velocity of the particle increases and approaches a significant fraction of the speed of light, relativistic effects must be considered. In relativity, the mass of the particle increases with velocity according to the equation:
m=m0√1−v2c2
where m0 is the rest mass, v is the velocity of the particle, and c is the speed of light.
Step 5: Analyze the implications of increasing velocity
As the velocity v approaches the speed of light c, the denominator in the mass equation decreases, causing the mass m to increase. Since the force F remains constant, but the mass m is increasing, the acceleration a must decrease:
a=Fm
As m increases, a decreases.
Conclusion
Initially, if the particle's velocity is much less than the speed of light, the acceleration remains constant. However, as the velocity increases and becomes comparable to the speed of light, the acceleration decreases. Therefore, the correct answer to the question is that the acceleration will gradually decrease.
Final Answer
The acceleration will gradually decrease.
According to Newton's second law of motion, the relationship between force (F), mass (m), and acceleration (a) is given by the equation:
F=m⋅a
This means that the force acting on an object is equal to the mass of the object multiplied by its acceleration.
The problem states that a constant force is acting on the particle. This implies that the value of F is constant. Additionally, we need to consider the mass of the particle. If the velocity of the particle is much less than the speed of light (non-relativistic speeds), the mass of the particle can be considered constant.
Since both the force (F) and mass (m) are constant (under non-relativistic conditions), we can rearrange the equation to find acceleration:
a=Fm
Since F is constant and m is constant, it follows that the acceleration (a) will also remain constant.
However, if the velocity of the particle increases and approaches a significant fraction of the speed of light, relativistic effects must be considered. In relativity, the mass of the particle increases with velocity according to the equation:
m=m0√1−v2c2
where m0 is the rest mass, v is the velocity of the particle, and c is the speed of light.
As the velocity v approaches the speed of light c, the denominator in the mass equation decreases, causing the mass m to increase. Since the force F remains constant, but the mass m is increasing, the acceleration a must decrease:
a=Fm
As m increases, a decreases.
Initially, if the particle's velocity is much less than the speed of light, the acceleration remains constant. However, as the velocity increases and becomes comparable to the speed of light, the acceleration decreases. Therefore, the correct answer to the question is that the acceleration will gradually decrease.
The acceleration will gradually decrease.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - THE SPECIAL THEORY OF RELATIVITYEXERCISE - Objective 21videos
THE SPECIAL THEORY OF RELATIVITY
- BOOK - HC VERMA ENGLISHCHAPTER - THE SPECIAL THEORY OF RELATIVITYEXERCISE - Exercise28videos
THE SPECIAL THEORY OF RELATIVITY
- BOOK - HC VERMA ENGLISHCHAPTER - THE SPECIAL THEORY OF RELATIVITYEXERCISE - worked out example8videos
THE SPECIAL THEORY OF RELATIVITY
- BOOK - HC VERMA ENGLISHCHAPTER - THE NUCLEOUSEXERCISE - Short answer12videos
THE NUCLEOUS
- BOOK - HC VERMA ENGLISHCHAPTER - THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENTEXERCISE - Short Question9videos
THERMAL AND CHEMICAL EFFECT OF ELECTRIC CURRENT
Similar Questions
A constant force acts on a particle and its displacement x (in cm) is related to the time t (in s) by the equation t=√x+3, when the velocity of the particle is zero, its displacement ( in cm) is
View SolutionThe momentum of a particle is P=A+Bt2 . Where , A and B are constant perpendicular vectors . The force acting on the particle when its acceleration is at 45∘ with its velocity is
(a)2√ABB (b)2B (c)zero (d)2AView SolutionWhen a force F acts on a particle of mass m, the acceleration of particle becomes a. now if two forces of magnitude 3F and 4F acts on the particle simultaneously as shown in figure, then the acceleration of the particle is
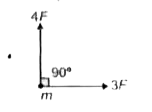 View Solution
View SolutionA force P acts on a particle so as to accelerate it from rest to certain velocity. If P is replaced then by Q which decelerates it to rest.
View SolutionA particle at rest on a frictionless table is acted upon by a horizontal force which is constant in magnitude and direction. A graph is plotted of the work done on the particle W, against the speed of the particle v. If there are no frictional forces acting on the particle, the graph will look like
View SolutionAccording to Newton.s second law of motion, resultant force on a particle is in the direction of acceleration of the particle. Two forcce F1andF2 are acting on a particle as shown in the figure. The acceleration of the particle is along X-axis. FInd the value of F1 (in newton)
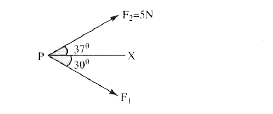 View Solution
View SolutionA particle of mass 70 g, moving at 50 cm/s , is acted upon by a variable force opposite to its direction of motion. The force F is shown as a function of time t
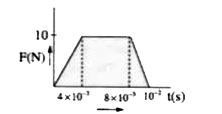
(a) its speed will be 50 cm/s after the force stops acting
(b) its direction of motion will reverse
(c) its average acceleration will be 1m/s2 during the interval in which the force acts
its average acceleration will be 10m/s2 during the interval in which the force actsView SolutionA force F1 acts on a particle so as to accelerate it from rest to a velocity v. The force F1 is then replaced by F2 which decelerates it to rest.
View SolutionA force F1 acts on a particle so as to accelerate it from rest to a velocity v. The force F1 is then replaced by F2 which decelerates it to rest
View SolutionUnder the action of a constant force, A particle is experiencing a constant acceleration. The power is
View Solution

