In the cyclotron, as radius of the circular path of the charged particle increase (ω = angular velocity, v = linear velocity)
Both ωandυ increase
only ω increase, υ remains constant
only υ increases , ω remains constant
υ increases, ω decreases
The correct Answer is:C
To solve the problem regarding the behavior of angular velocity and linear velocity in a cyclotron as the radius of the circular path of a charged particle increases, we can follow these steps:
1. Understanding the Cyclotron:
A cyclotron is a device that accelerates charged particles using a magnetic field. The charged particle moves in a circular path due to the Lorentz force exerted by the magnetic field.
2. Identify the Key Relationships:
- The linear velocity v of the charged particle in a cyclotron is given by the formula:
v=Bqrm
where:
- B = magnetic field strength
- q = charge of the particle
- r = radius of the circular path
- m = mass of the particle
- The angular velocity ω is given by:
ω=vr
3. Analyzing the Effect of Increasing Radius:
- If the radius r increases, we can analyze how it affects v and ω.
- From the equation for linear velocity:
v=Bqrm
Since B, q, and m are constants, an increase in r will lead to a proportional increase in v. Thus, v increases as r increases.
4. Analyzing Angular Velocity:
- Now, substituting the expression for v into the equation for ω:
ω=vr=Bqr/mr=Bqm
- Here, B, q, and m are constants, meaning that ω does not depend on r. Therefore, ω remains constant even as r increases.
5. Conclusion:
- As the radius r of the circular path increases, the linear velocity v increases, while the angular velocity ω remains constant.
Final Answer:
- Linear velocity v increases.
- Angular velocity ω remains constant.
A cyclotron is a device that accelerates charged particles using a magnetic field. The charged particle moves in a circular path due to the Lorentz force exerted by the magnetic field.
- The linear velocity v of the charged particle in a cyclotron is given by the formula:
v=Bqrm
where:
- B = magnetic field strength
- q = charge of the particle
- r = radius of the circular path
- m = mass of the particle
ω=vr
- If the radius r increases, we can analyze how it affects v and ω.
- From the equation for linear velocity:
v=Bqrm
Since B, q, and m are constants, an increase in r will lead to a proportional increase in v. Thus, v increases as r increases.
- Now, substituting the expression for v into the equation for ω:
ω=vr=Bqr/mr=Bqm
- Here, B, q, and m are constants, meaning that ω does not depend on r. Therefore, ω remains constant even as r increases.
- As the radius r of the circular path increases, the linear velocity v increases, while the angular velocity ω remains constant.
- Linear velocity v increases.
- Angular velocity ω remains constant.
Similar Questions
In a cyclotron, the angular frequency of a charged particle is independent
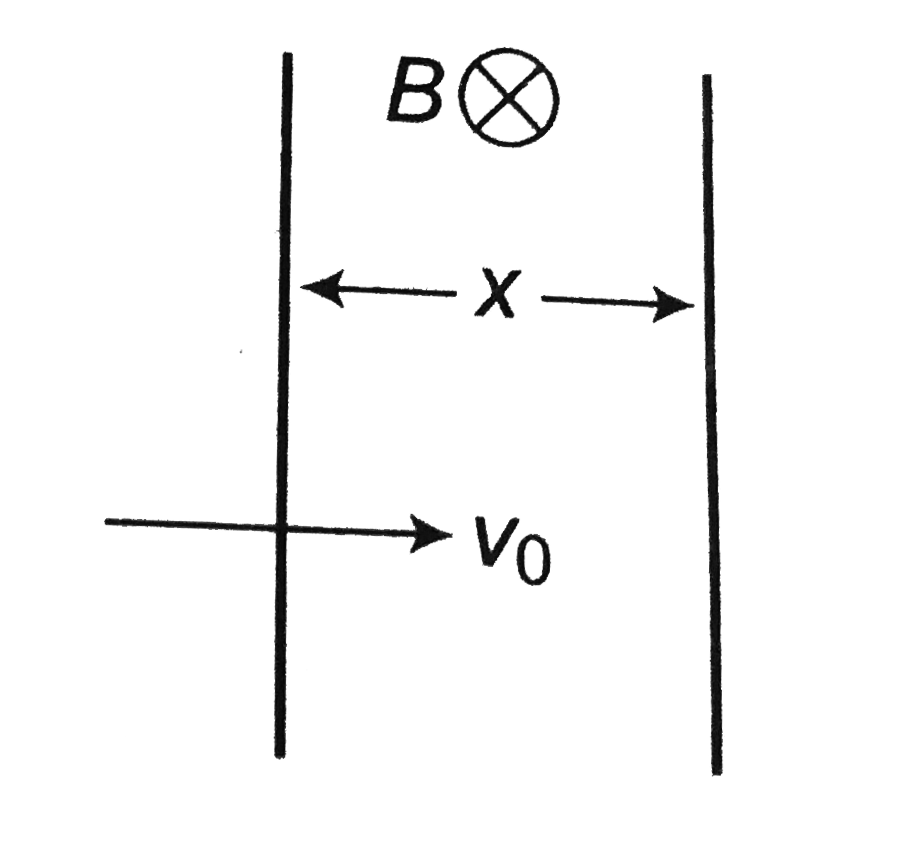
View SolutionA charged particle enters into a uniform magnetic field with velocity v0 perpendicular to it , the length of magnetic field is x=√32R, where R is the radius of the circular path of the particle in the field .The magnitude of charge in velocity of the particle when it comes out of the field is
View Solution
Knowledge Check
A charged particle is moving in a cyclotron, what effect on the radius of path of this charged particle will occur when the frequency of the radio frequency field is doubled?
AIt will also be doubled.BIt will be halved.CIt will be increased by four times.DIt will remain unchanged.
A charged particle enters a uniform magnetic field with velocity v0=4m/s perpendicular to it, the length of magnetic field is x=(√32)R, where R is the radius of the circular path of the particle in the field. Find the magnitude of charge in velocity (in m/s) of the particle when it comes out of the field.
View SolutionThe angular velocity of a particle moving in a circle realative to the center of the circle is equal to ω. Find the angular velocity of the particle relative to a point on the circular path.
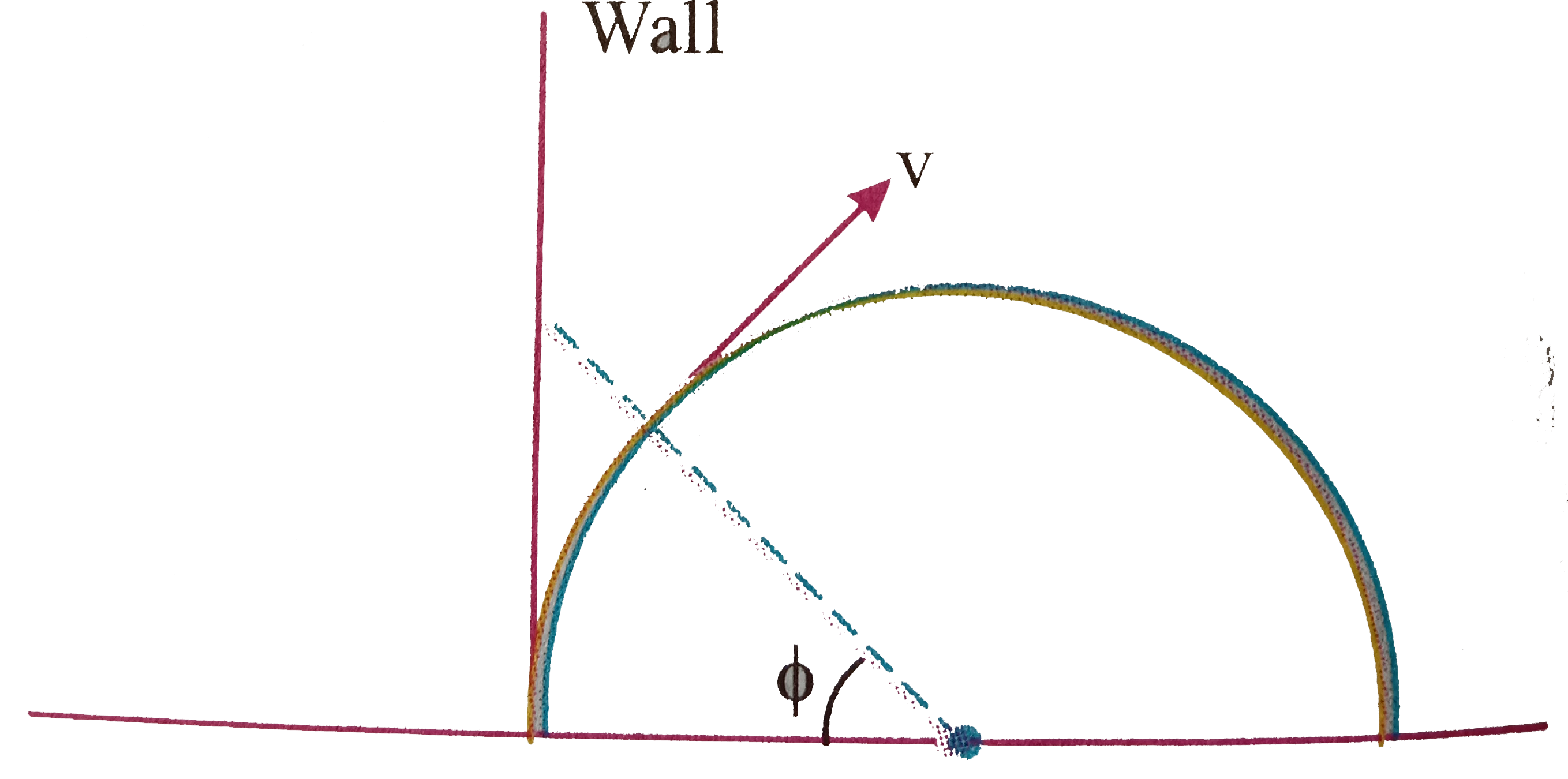
View SolutionOn a particle moving on a circular path with constant speed v, light is thrown from a projectors placed at the centre of the circular path. The shadow of the particle is formed on the wall. The velocity of shadow up the wall is
View SolutionAssertion: In circular motion, dot product of velocity vector (v) and acceleration vector (a) may be positive, negative or zero.
Reason: Dot product of angular velocity vector and linear velocity vector is always zero.
View SolutionA body is in pure rotation. The linear speed 'v' of a particle, the distance 'r' of the particle from the axis and the angular velocity ω of the body are related as ω=vr. Thus
View SolutionA billiard ball of mass m and radius r, when hit in a horizontal direction by a cue at a height h above its centre, acquired a linear velocity v0. The angular velocity ω0 acquired by the ball is
View SolutionA particle is moving on a circular path such that at any instant its position vector, linear velocity. Angular velocity, angular acceleration with respect to centre are →r,→v,→w,→α respectively. Net acceleration of the particle is :−
View Solution
