A particle is moving on a circular path such that at any instant its position vector, linear velocity. Angular velocity, angular acceleration with respect to centre are →r,→v,→w,→α respectively. Net acceleration of the particle is :−
(→ω×→v)−(→r×→α)
(→ω×→v)+(→r×→α)
(→v×→ω)+(→r×→α)
(→v×→ω)−(→r×→α)
The correct Answer is:A
To find the net acceleration of a particle moving in a circular path, we need to consider both the centripetal (or radial) acceleration and the tangential acceleration.
1. Identify the Components of Acceleration:
- The net acceleration of the particle in circular motion can be expressed as the sum of centripetal acceleration and tangential acceleration.
- Centripetal acceleration (→ac) is directed towards the center of the circular path and is given by the formula:
→ac=v2r^r=ω2r^r
where v is the linear velocity, r is the radius of the circular path, and ^r is the unit vector pointing radially inward.
2. Tangential Acceleration:
- The tangential acceleration (→at) is due to the change in the speed of the particle along the circular path and is given by:
→at=α×r
where α is the angular acceleration.
3. Net Acceleration:
- The net acceleration (→a) of the particle can be expressed as the vector sum of the centripetal and tangential accelerations:
→a=→ac+→at
- Substituting the expressions for →ac and →at:
→a=v2r^r+α×r
4. Final Expression:
- Therefore, the net acceleration of the particle moving in a circular path can be expressed as:
→a=v2r^r+α×→r
- The net acceleration of the particle in circular motion can be expressed as the sum of centripetal acceleration and tangential acceleration.
- Centripetal acceleration (→ac) is directed towards the center of the circular path and is given by the formula:
→ac=v2r^r=ω2r^r
where v is the linear velocity, r is the radius of the circular path, and ^r is the unit vector pointing radially inward.
- The tangential acceleration (→at) is due to the change in the speed of the particle along the circular path and is given by:
→at=α×r
where α is the angular acceleration.
- The net acceleration (→a) of the particle can be expressed as the vector sum of the centripetal and tangential accelerations:
→a=→ac+→at
- Substituting the expressions for →ac and →at:
→a=v2r^r+α×r
- Therefore, the net acceleration of the particle moving in a circular path can be expressed as:
→a=v2r^r+α×→r
Topper's Solved these Questions
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLENCHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
The angular velocity and angular acceleration of the pivoted rod are given as ω and α respectively. Fid the x and y components of acceleration of B.
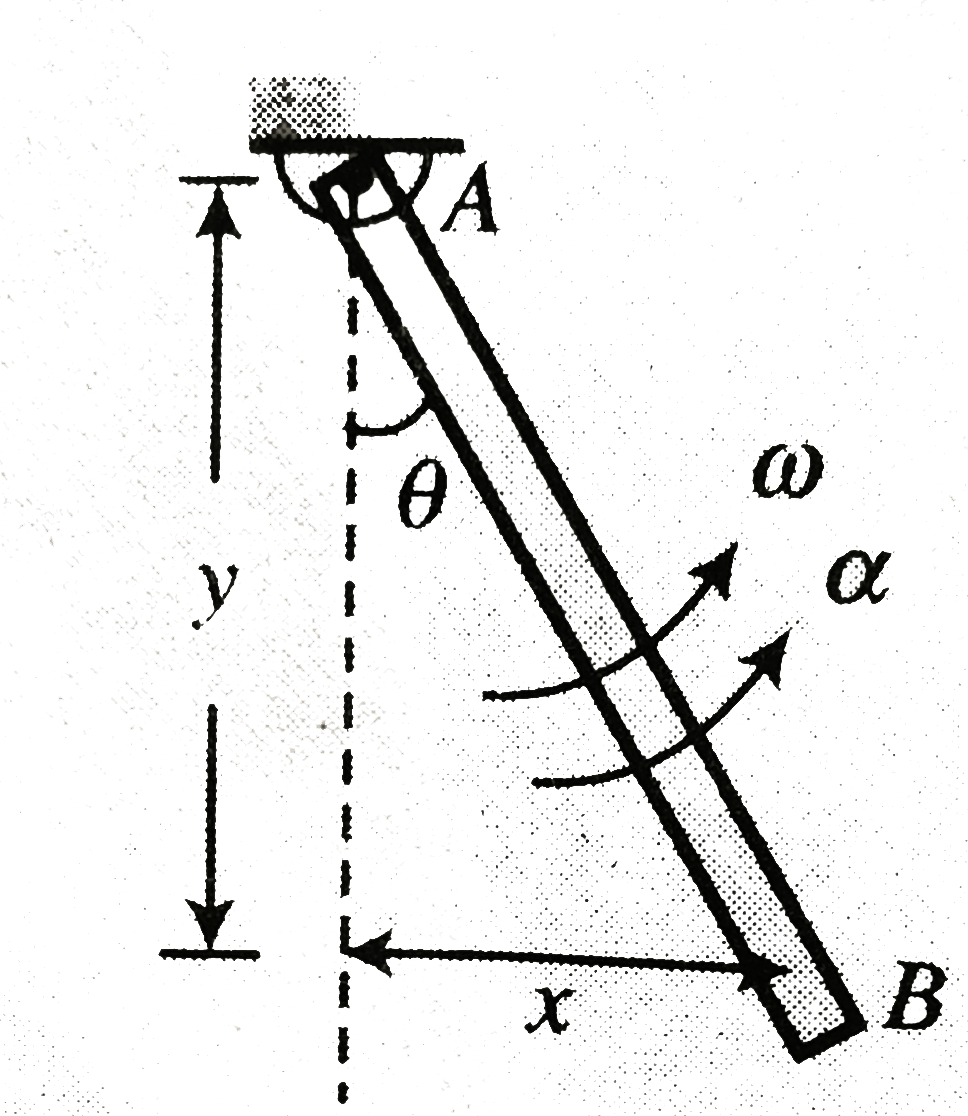
View SolutionIf a particle is moving on a circular path with constant speed, then the angle between the direction of acceleration and its position vector w.r.t. centre of circle will be
View SolutionA particle is moving along a circular path. The angular velocity, linear velocity, Angular acceleration, and centripetal acceleration of the particle at any instant. Respectively are →ω,→v,→∝,and→ac. Which of the following relations is not correct ?
View SolutionA particle is moving around a circular path with uniform angular speed (x) . The radius of the circular path is (r). The acceleration of the particle is:
View SolutionA particle is moving along a circle and its linear velocity is 0.5ms when its angular velocity is 2.5rads−1. Its tangential acceleration is 0.2ms−2 then its angular acceleration is
View SolutionA particle starts moving in a circular path of radius R with an initial speed v0 clockwise. If the angular acceleration is αrad/s2 anticlockwise, the time when the acceleration and the velocity vectors of the particle become parallel, is
View SolutionA particle moves in a circle with constant angular velocity ω about a point P on its circumference. The angular velocity of the particle about the centre C of the circle is
View SolutionA particle moves in a circle of radius r with angular velocity ω. At some instant its velocity is v radius vector with respect to centre of the circle is r. At this particular instant centripetal acceleration ac of the particle would be
View SolutionIf a particle is moving as →r=(→i+2→j)cosω0t then,motion of the particleis
View SolutionIn the cyclotron, as radius of the circular path of the charged particle increase (ω = angular velocity, v = linear velocity)
View Solution
