Under the action of a constant force, A particle is experiencing a constant acceleration. The power is
Positive constant
Negative constant
Increasing uniformly with time
Decreasing uniformly with time
The correct Answer is:C
To solve the problem, we need to analyze the situation where a particle is under the influence of a constant force, resulting in constant acceleration. We will derive the expression for power in this context step by step.
Step 1: Understand the relationship between force, mass, and acceleration
According to Newton's second law, the acceleration a of a particle is given by:
a=Fm
where F is the constant force acting on the particle and m is its mass.
Hint: Remember that acceleration is directly proportional to the force applied and inversely proportional to the mass of the object.
Step 2: Determine the velocity of the particle
If the particle starts from rest, its initial velocity u=0. The velocity v after time t can be expressed as:
v=u+at=0+(Fm)t=Fmt
Hint: Use the kinematic equation for velocity when starting from rest, which simplifies to v=at.
Step 3: Calculate the power
Power P is defined as the rate at which work is done, and it can also be expressed as the product of force and velocity:
P=F⋅v
Substituting the expression for velocity we found in Step 2:
P=F⋅(Fmt)=F2mt
Hint: Power is the product of force and the instantaneous velocity of the object.
Step 4: Analyze the relationship of power with time
From the derived equation P=F2mt, we can see that power is directly proportional to time t. This means as time increases, power also increases linearly.
Hint: Look for the relationship between power and time; in this case, it is linear.
Conclusion
The power experienced by the particle under the action of a constant force and constant acceleration increases uniformly with time. Therefore, the correct answer is that the power increases uniformly with time.
Final Answer: The power is increasing uniformly with time.
According to Newton's second law, the acceleration a of a particle is given by:
a=Fm
where F is the constant force acting on the particle and m is its mass.
If the particle starts from rest, its initial velocity u=0. The velocity v after time t can be expressed as:
v=u+at=0+(Fm)t=Fmt
Power P is defined as the rate at which work is done, and it can also be expressed as the product of force and velocity:
P=F⋅v
Substituting the expression for velocity we found in Step 2:
P=F⋅(Fmt)=F2mt
From the derived equation P=F2mt, we can see that power is directly proportional to time t. This means as time increases, power also increases linearly.
The power experienced by the particle under the action of a constant force and constant acceleration increases uniformly with time. Therefore, the correct answer is that the power increases uniformly with time.
Similar Questions
A particle of mass m moves from rest under the action of a constant force F which acts for two seconds. The maximum power attained is
View SolutionIf a constant force acts on a particle, its acceleration will
View SolutionA body moves under the action of a constant force along a straight line. The instantaneous power developed by this force with time t is correctly represented by.
View SolutionAn object of mass m, initially at rest under the action of a constant force F attains a velocity v in time t. Then, the average power supplied to mass is
View SolutionA particle starts its motion from rest under the action of a constant force. If the distance covered in first 10s is s1 and the covered in the first 20s is s2, then.
View SolutionA particle start moving from rest state along a straight line under the action of a constant force and travel distance x in first 5 seconds. The distance travelled by it in next five seconds will be
View SolutionA car of mass M is accelerating on a level smooth road under the action of a single force F acting along the direction of motion. The power delivered to the car is constant and equal to p. If the velocity of the car at an instant is v, then after travelling a distance of 7Mv33p the velocity become kv where k is__________.
View SolutionThe displacement x of particle moving in one dimension, under the action of a constant force is related to the time t by the equation t=√x+3
where xis∈metersandt∈seconds . Find
(i) The displacement of the particle when its velocity is zero , and
(ii) The work done by the force in the first 6seconds.
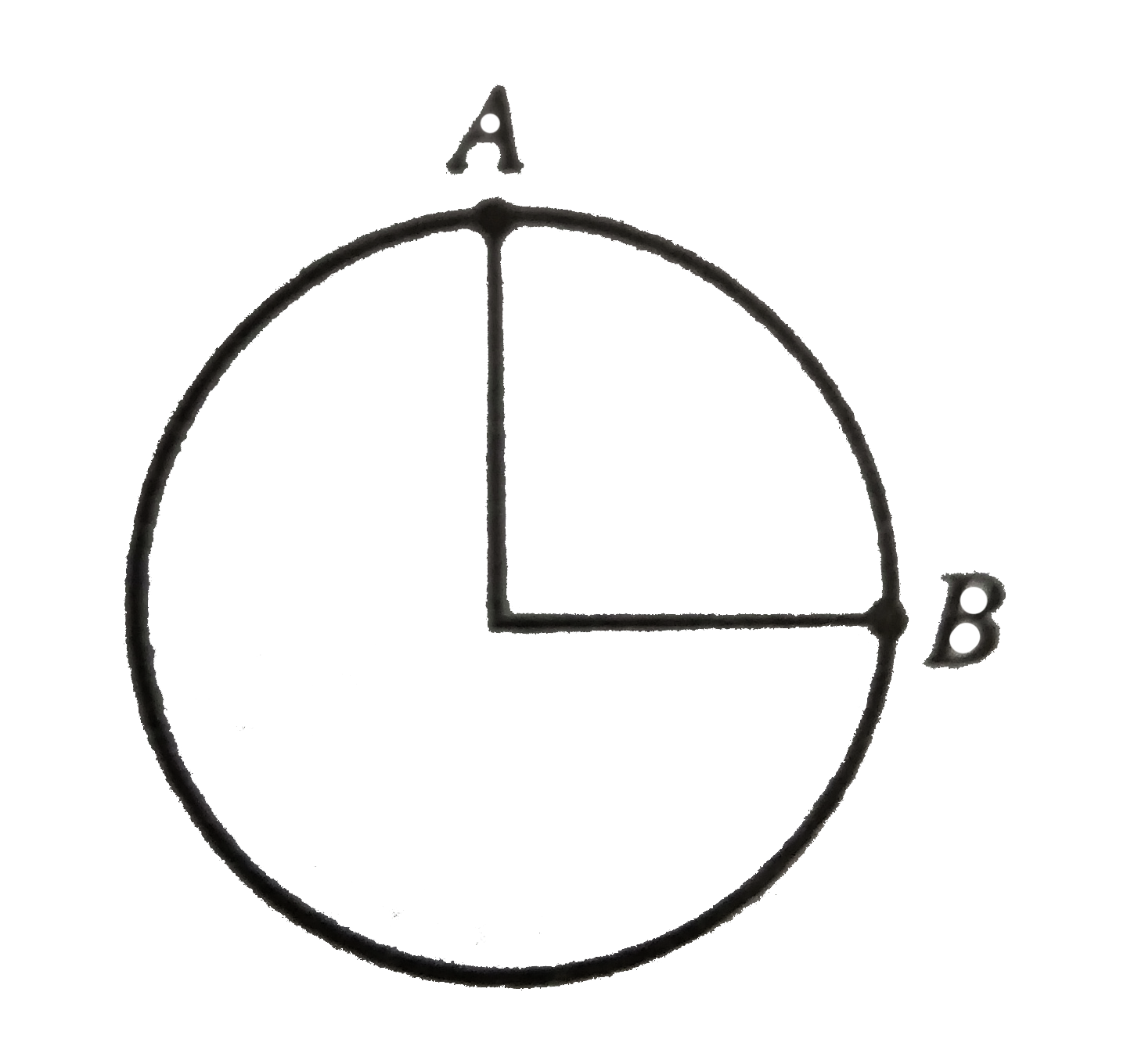
View SolutionA particle is moving in a circular path of radius 1 m. under the action of a centripetal force, the speed √2πms−1 of the particle is constant. Find the average of the velocity (inms−1) between A and B.
View SolutionA particle starts from origin at t=0 with a velocity of 15ˆims−1 and moves in xy-plane under the action of a force which produces a constant acceleration of 15ˆi+20ˆjms−2. Find the y-coordinate of the particle at the instant its x-coordinate is 180 m.
View Solution
