For a circular cardboard of uniform thickness and mass M, a square disc of the maximum possible are is cut. If the moment of inertia of the square with the moment of inertial of the square with the axis of rotation at the centre and perpendicular to the plane of the disc is Ma26, the radius of the circular cardboard is
√2a
a√2
2a
2√2a
The correct Answer is:B
To solve the problem, we need to find the radius R of the circular cardboard from which the maximum possible square disc is cut. We are given that the moment of inertia of the square is Ma26, where a is the side length of the square.
1. Understand the Moment of Inertia of the Square:
The moment of inertia I of a square plate about an axis through its center and perpendicular to its plane is given by:
I=M′a26
where M′ is the mass of the square and a is the side length of the square.
2. Relate the Mass of the Square to the Mass of the Circular Cardboard:
Since the square is cut from the circular cardboard, we can denote the mass of the square as M′ and the mass of the circular cardboard as M. The mass of the square M′ can be expressed in terms of the mass density and area, but we will focus on the relationship with the radius.
3. Determine the Side Length of the Square:
The maximum size of the square that can be cut from the circular cardboard is when its diagonal is equal to the diameter of the circle. The diagonal d of the square can be expressed as:
d=a√2
The diameter of the circular cardboard is 2R. Therefore, we have:
a√2=2R
From this, we can solve for a:
a=2R√2=R√2
4. Substituting the Side Length into the Moment of Inertia Equation:
Now substituting a=R√2 into the moment of inertia equation:
I=M′(R√2)26=M′⋅2R26=M′R23
We know from the problem statement that I=Ma26. Thus, we equate:
M′R23=M(R√2)26
Simplifying the right side:
M(2R2)6=MR23
5. Equating the Two Expressions:
Now we can set the two expressions equal to each other:
M′R23=MR23
Since R2 is common and non-zero, we can cancel it out:
M′=M
6. Finding the Radius:
Since M′ is the mass of the square and M is the mass of the circular cardboard, we have established that the maximum square that can be cut has a relationship with the radius R.
From the earlier equation a=R√2 and substituting back, we can find:
R=a√2
Final Answer:
Thus, the radius R of the circular cardboard is:
R=a√2
The moment of inertia I of a square plate about an axis through its center and perpendicular to its plane is given by:
I=M′a26
where M′ is the mass of the square and a is the side length of the square.
Since the square is cut from the circular cardboard, we can denote the mass of the square as M′ and the mass of the circular cardboard as M. The mass of the square M′ can be expressed in terms of the mass density and area, but we will focus on the relationship with the radius.
The maximum size of the square that can be cut from the circular cardboard is when its diagonal is equal to the diameter of the circle. The diagonal d of the square can be expressed as:
d=a√2
The diameter of the circular cardboard is 2R. Therefore, we have:
a√2=2R
From this, we can solve for a:
a=2R√2=R√2
Now substituting a=R√2 into the moment of inertia equation:
I=M′(R√2)26=M′⋅2R26=M′R23
We know from the problem statement that I=Ma26. Thus, we equate:
M′R23=M(R√2)26
Simplifying the right side:
M(2R2)6=MR23
Now we can set the two expressions equal to each other:
M′R23=MR23
Since R2 is common and non-zero, we can cancel it out:
M′=M
Since M′ is the mass of the square and M is the mass of the circular cardboard, we have established that the maximum square that can be cut has a relationship with the radius R.
R=a√2
Thus, the radius R of the circular cardboard is:
R=a√2
Similar Questions
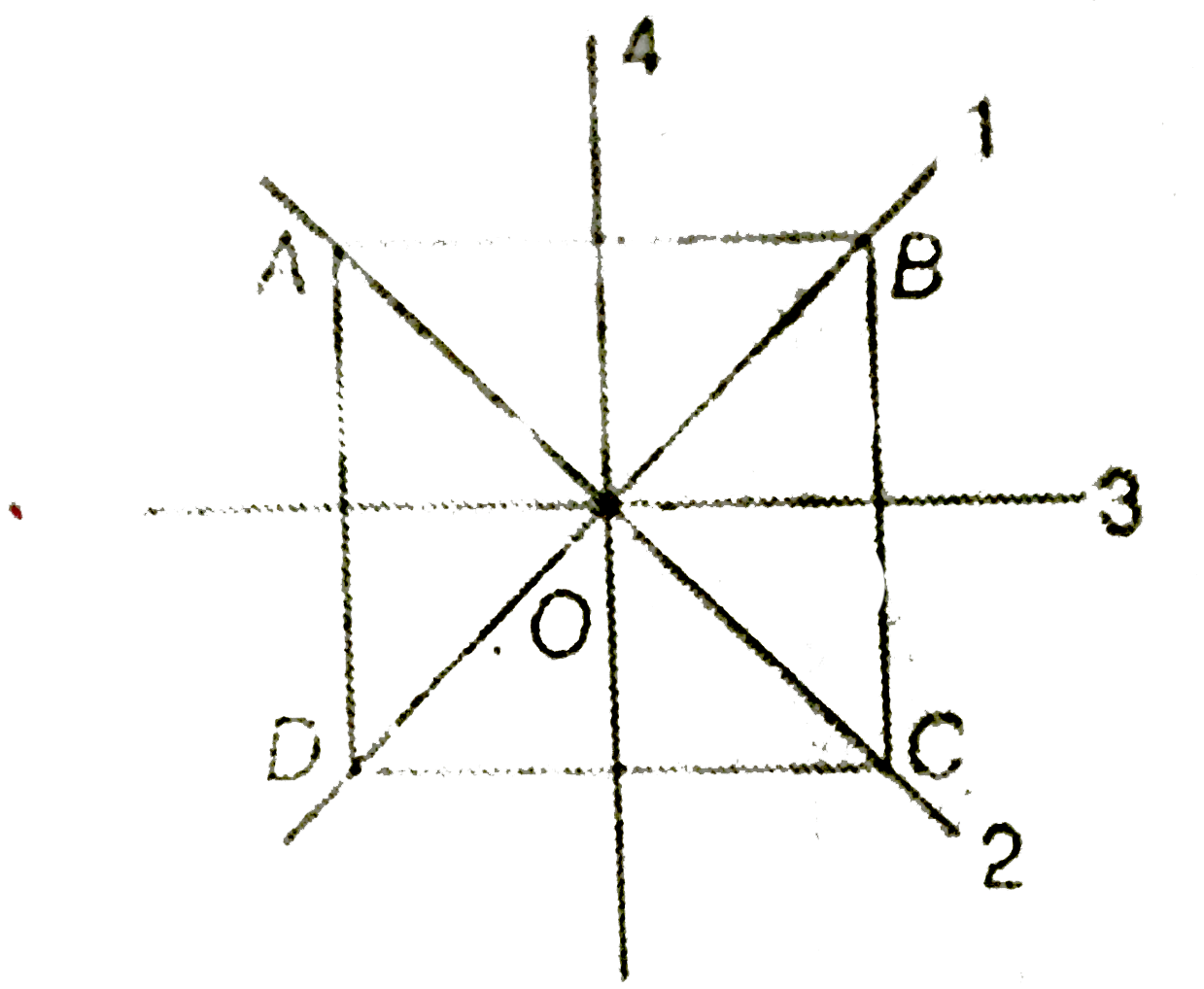
The moment of inertia of a thin square plate ABCD of uniform thickness about an axis passing through the centre O and perpendicular to plate is
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionThe diagram shows a uniform disc of mass M & radius 'a', if the moment of inertia of the disc about the axis XY is I, its moment of inertia about an axis through O and perpendicular to the plane of the disc is

View SolutionSurface mass density of disc of mass m and radius R is Kr2. Then its moment of inertia w.r.t. axis of rotation passing through center and perpendicular to the plane of disc is :
View SolutionA disc has mass 9 m. A hole of radius R/3 is cut from it as shown in the figure. The moment of inertia of remaining part about an axis passing through the centre 'O' of the disc and perpendicular to the plane of the disc is :

View SolutionFind the moment of inertia of a uniform square plate of mass M and edge of length 'l' about its axis passing through P and perpendicular to it.

View SolutionThe moment of inertia of a uniform semicircular disc of mass M and radius r about a line perpendicular to the plane of the disc through the center is
View SolutionThe mass of a disc is 700 gm and its radius of gyration is 20 cm. What is its moment of inertia if it rotates about an axis passing through its centre and perpendicular to the face of the disc?
View SolutionCalculate the moment of inertia of a.unifprm disc of mass 0.4 kg and radius 0.1m about an axis passing through its edge and perpendicular to the plane of die disc ?
View Solution
