The activation energies of two reactions are and with . If the temperature of the reacting systems is increased from to , which of the following is correct?
The correct Answer is:C
To solve the problem, we need to analyze the effect of temperature on the rate constants of two reactions with different activation energies. Let's break it down step by step.
Step 1: Understand the relationship between rate constant and activation energy
The rate constant k of a reaction is related to the activation energy Ea and temperature T by the Arrhenius equation:
k=Ae−EaRT
where A is the pre-exponential factor, R is the gas constant, and T is the temperature in Kelvin.
Step 2: Write the expression for the change in rate constant with temperature
When the temperature changes from T to T′, the new rate constants k′1 and k′2 for the two reactions can be expressed as:
logk′1k1=Ea1R(1T−1T′)
logk′2k2=Ea2R(1T−1T′)
Step 3: Compare the two reactions
Since it is given that Ea1>Ea2, we can analyze the implications:
- The term Ea1R(1T−1T′) will be larger than Ea2R(1T−1T′) when T′>T.
- This means that the increase in the rate constant k′1 for the reaction with higher activation energy Ea1 will be less pronounced compared to the increase in k′2 for the reaction with lower activation energy Ea2.
Step 4: Conclusion
From the above analysis, we can conclude that:
k′1k1<k′2k2
This implies that the rate constant for the reaction with the lower activation energy increases more significantly with the increase in temperature than that of the reaction with the higher activation energy.
Final Answer
Thus, the correct conclusion is that the reaction with lower activation energy (reaction 2) will have a greater increase in its rate constant compared to the reaction with higher activation energy (reaction 1) when the temperature is increased from T to T′.
The rate constant k of a reaction is related to the activation energy Ea and temperature T by the Arrhenius equation:
k=Ae−EaRT
where A is the pre-exponential factor, R is the gas constant, and T is the temperature in Kelvin.
When the temperature changes from T to T′, the new rate constants k′1 and k′2 for the two reactions can be expressed as:
logk′1k1=Ea1R(1T−1T′)
logk′2k2=Ea2R(1T−1T′)
Since it is given that Ea1>Ea2, we can analyze the implications:
- The term Ea1R(1T−1T′) will be larger than Ea2R(1T−1T′) when T′>T.
- This means that the increase in the rate constant k′1 for the reaction with higher activation energy Ea1 will be less pronounced compared to the increase in k′2 for the reaction with lower activation energy Ea2.
From the above analysis, we can conclude that:
k′1k1<k′2k2
This implies that the rate constant for the reaction with the lower activation energy increases more significantly with the increase in temperature than that of the reaction with the higher activation energy.
Thus, the correct conclusion is that the reaction with lower activation energy (reaction 2) will have a greater increase in its rate constant compared to the reaction with higher activation energy (reaction 1) when the temperature is increased from T to T′.
Similar Questions
The rate of reaction increases isgnificantly with increase in temperature. Generally, rate of reactions are doubled for every 10∘C rise in temperature. Temperature coefficient gives us an idea about the change in the rate of a reaction for every 10∘C change in temperature.
Temperature coefficient(μ)=Rate constant of(T+10)∘CRate constant atT∘C
Arrhenius gave an equation which describes aret constant k as a function of temperature
k=Ae−Ea/RT
where k is the rate constant, A is the frequency factor or pre-exponential factor, Ea is the activation energy, T is the temperature in kelvin, R is the universal gas constant.
Equation when expressed in logarithmic form becomes
logk=logA−Ea2.303RT
Activation energies of two reaction are Ea and Ea' with Ea>E'a. If the temperature of the reacting systems is increased form T1 to T2 (k' is rate constant at higher temperature).
View SolutionThe activation energies of two reactions are E1 & E2 with E1>E2. If temperature of reacting system is increased from T1 (rate constant are k1 and k2) to T2 (rate constant are k11 and k12) predict which of the following alternative is correct.
View SolutionThe activity of a sample of a radioactive meterial is A1 , at time t1 , and A2 at time t2(t2>t1) . If its mean life T, then
View SolutionActivation energy (Ea) and rate constants (k1 and k2) of a chemical reaction at two different temperatures (T1 and T2) are related by
View SolutionAtomic masses of two heavy atoms are A1 and A2. Ratio of their respective nuclear densities will be approximately
View SolutionThe rate of a reaction depends upon the temperature and is quantitatively expressed as
k=Ae−EaRT
i) If a graph is plotted between log k and 1/T, write the expression for the slope of the reaction?
ii) If at under different conditions Ea1andEa2 are the activation energy of two reactions. If Ea1=40J/mol andEa2=80J/ mol. Which of the two has a larger value of the rate constant?
View SolutionA colliison between reactant molecules must occur with a certain minimum energy before it is effective in yielding Product molecules. This minimum energy is called activation energy Ea Large the value of activation energy, smaller the value of rate constant k. Larger is the value of activation energy, greater is the effect of temperature rise on rate constant k.
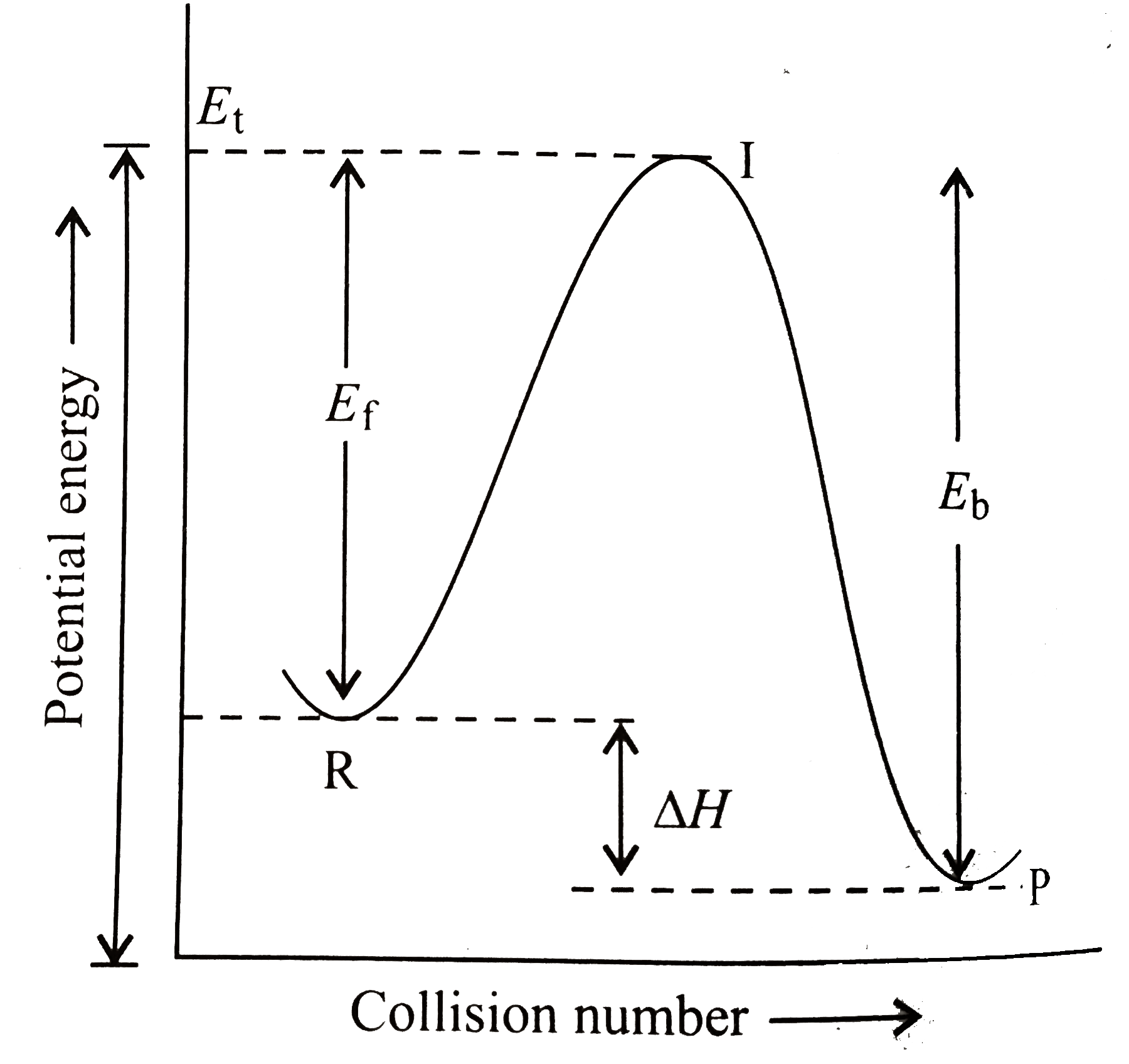
Ef= Activation energy of forward reaction
Eb= Activation energy of backward reaction
ΔH=Ef−Eb
Ef= threshold energy
For two reactions, activation energies are Ea1 and Ea2, rate constant are k1 and k2 at the same temperature. If k1>k2, then
View SolutionThe capacitance of the capacitors of plate areas A1 and A2(A1<A2) at a distance d is

View SolutionThe capacitance of capacitor of plate areas A1 and A2 (A1<A2 at a distance d is

View SolutionIn the following circuit readings in ammeters A1 and A2 will be -

View Solution