Four identical spheres each of radius 10 cm and mass 1 kg are placed on a horizontal surface touching one another so that their centres are located at the corners of square of side 20 cm. What is the distance of their centre of mass from centre of either sphere ?
5 cm
10 cm
20 cm
10√2cm
The correct Answer is:D
To find the distance of the center of mass from the center of either sphere, we can follow these steps:
Step 1: Understand the Configuration
We have four identical spheres, each with a radius of 10 cm and mass of 1 kg. They are arranged such that their centers form the corners of a square with a side length of 20 cm.
Step 2: Identify the Coordinates of the Centers
Let's assign coordinates to the centers of the spheres:
- Sphere 1 (bottom left corner): (0,0)
- Sphere 2 (bottom right corner): (20,0)
- Sphere 3 (top left corner): (0,20)
- Sphere 4 (top right corner): (20,20)
Step 3: Calculate the Center of Mass
The center of mass (CM) for a system of particles can be calculated using the formula:
CM=1M∑mi→ri
where M is the total mass and →ri are the position vectors of the masses.
In our case, since all spheres have the same mass m=1kg, the total mass M=4kg.
The coordinates of the center of mass can be calculated as:
xCM=1M∑mixi=14(0+20+0+20)=404=10cm
yCM=1M∑miyi=14(0+0+20+20)=404=10cm
Thus, the center of mass is located at (10,10).
Step 4: Calculate the Distance from the Center of Either Sphere
Now, we need to find the distance from the center of one of the spheres (for example, Sphere 1 at (0,0)) to the center of mass (10,10).
Using the distance formula:
d=√(xCM−xsphere)2+(yCM−ysphere)2
Substituting the values:
d=√(10−0)2+(10−0)2=√102+102=√100+100=√200=10√2cm
Final Answer
The distance of the center of mass from the center of either sphere is 10√2cm.
---
We have four identical spheres, each with a radius of 10 cm and mass of 1 kg. They are arranged such that their centers form the corners of a square with a side length of 20 cm.
Let's assign coordinates to the centers of the spheres:
- Sphere 1 (bottom left corner): (0,0)
- Sphere 2 (bottom right corner): (20,0)
- Sphere 3 (top left corner): (0,20)
- Sphere 4 (top right corner): (20,20)
The center of mass (CM) for a system of particles can be calculated using the formula:
CM=1M∑mi→ri
where M is the total mass and →ri are the position vectors of the masses.
xCM=1M∑mixi=14(0+20+0+20)=404=10cm
yCM=1M∑miyi=14(0+0+20+20)=404=10cm
Now, we need to find the distance from the center of one of the spheres (for example, Sphere 1 at (0,0)) to the center of mass (10,10).
d=√(xCM−xsphere)2+(yCM−ysphere)2
Substituting the values:
d=√(10−0)2+(10−0)2=√102+102=√100+100=√200=10√2cm
The distance of the center of mass from the center of either sphere is 10√2cm.
Similar Questions
Three identical spheres each of radius .R. are placed on a horizontal surface touching one another. If one of the spheres is removed, the shift in the centre of mass of the system is
View SolutionFour point masses are placed at the corners of a square of side 2 m as shown in the figure. Find the centre of mass of the system w.r.t. the centre of square.

View Solution
Knowledge Check
Four particles each of mass m are placed at the vertices of a square of side l. the potential at the centre of square is
A−√2Gm2l(2−1√2)B−2Gm2l(2+1√2)C−√2Gm2l(√2−1√2)D−2Gm2l(√2−1√2)
Three identical spheres each of radius .R. are placed touching each other so that their centres A, B and C lie on a straight line. The position of their centre of mass from A is
View SolutionFour equal masses (each of mass M) are placed at the corners of a square of side a. The escape velocity of a body from the centre O of the square is
View SolutionFour point charges are placed at the corners of a square ABCD of side 10 cm, as shown in figure. The force on a charge of 1μC placed at the centre of square is

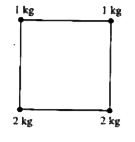
View SolutionFour point masses 1 kg, 1 kg, 2 kg and 2 kg are placed at the corners of a square of side a m as shown in Fig. Find the centre of mass of the system.
View SolutionA solid sphere of radius R is placed on a cube of side 2R. Both are made of same material. Find the distance of their centre of mass fro the interface.
View SolutionFour particles of masses 1kg, 2kg, 3kg and 4kg are placed at the four vertices A,B,C and D of a square of side 1m. Find square of distance of their centre of mass from A.
View SolutionFour particles of masses 2,2,4,4 kg are arranged at the corners A,B,C,D of a square ABCD of side 2m as shown in the figure. The perpendicular distance of their centre of mass from the side AB is

View Solution
