A fixed mass of a gas is first heated isobarically to double the volume and then cooled isochorically to decrease the temperature back to the initial value. By what factor would the work done by the decreased, had the process been isothermal?
2
ln 2
ln 3
The correct Answer is:C
To solve the problem, we need to analyze the two processes: the isobaric process followed by the isochoric process, and then compare it to an isothermal process.
1. Understanding the Initial Conditions:
- Let the initial volume of the gas be V0 and the initial pressure be P0.
- The initial temperature is T0.
2. Isobaric Heating to Double the Volume:
- The gas is heated isobarically (at constant pressure) to double its volume. Therefore, the final volume after this process becomes:
Vf=2V0
- Since the process is isobaric, the work done W1 during this process can be calculated using the formula:
W1=PΔV=P0(Vf−V0)=P0(2V0−V0)=P0V0
3. Isochoric Cooling to Initial Temperature:
- After reaching 2V0, the gas is cooled isochorically (at constant volume) to return to the initial temperature T0.
- During this isochoric process, no work is done since the volume remains constant:
W2=0
4. Total Work Done in the Given Process:
- The total work done in the entire process (isobaric followed by isochoric) is:
Wtotal=W1+W2=P0V0+0=P0V0
5. Isothermal Process:
- Now, let's consider the hypothetical scenario where the gas undergoes an isothermal process from the initial state (V0,T0) to the final state (2V0,T0).
- The work done Wisothermal in an isothermal process is given by:
Wisothermal=nRTln(VfVi)
- Here, since nRT=P0V0 at the initial state, we can express the work done as:
Wisothermal=P0V0ln(2V0V0)=P0V0ln(2)
6. Comparing Work Done:
- Now, we need to find the factor by which the work done in the original process decreases compared to the isothermal process:
Factor=WisothermalWtotal=P0V0ln(2)P0V0=ln(2)
Final Answer:
The factor by which the work done decreases if the process had been isothermal is:
Factor=ln(2)
- Let the initial volume of the gas be V0 and the initial pressure be P0.
- The initial temperature is T0.
- The gas is heated isobarically (at constant pressure) to double its volume. Therefore, the final volume after this process becomes:
Vf=2V0
- Since the process is isobaric, the work done W1 during this process can be calculated using the formula:
W1=PΔV=P0(Vf−V0)=P0(2V0−V0)=P0V0
- After reaching 2V0, the gas is cooled isochorically (at constant volume) to return to the initial temperature T0.
- During this isochoric process, no work is done since the volume remains constant:
W2=0
- The total work done in the entire process (isobaric followed by isochoric) is:
Wtotal=W1+W2=P0V0+0=P0V0
- Now, let's consider the hypothetical scenario where the gas undergoes an isothermal process from the initial state (V0,T0) to the final state (2V0,T0).
- The work done Wisothermal in an isothermal process is given by:
Wisothermal=nRTln(VfVi)
- Here, since nRT=P0V0 at the initial state, we can express the work done as:
Wisothermal=P0V0ln(2V0V0)=P0V0ln(2)
- Now, we need to find the factor by which the work done in the original process decreases compared to the isothermal process:
Factor=WisothermalWtotal=P0V0ln(2)P0V0=ln(2)
The factor by which the work done decreases if the process had been isothermal is:
Factor=ln(2)
Similar Questions
Two moles of an ideal gas at temperature T0=300K was cooled isochorically so that the pressure was reduced to half. Then, in an isobaric process, the gas expanded till its temperature got back to the initial value. Find the total amount of heat absorbed by the gas in the processs
View SolutionIn a flexible balloon 2, moles of SO2 having an initial volume of 1 kL at a temperature of 27.∘C is filled . The gas is first expanded to thrice its initial volume isobarically and then further expanded adiabatically so as to attain its initial temperature . Assuming the gas to be ideal , the work done by the gas in the whole process is [γSO2=43,R=253Jmol−1K−1]
View SolutionTwo moles of a certain gas at a temperature T0=300K were cooled isochorically so that the pressure of the gas got reduced 2 times. Then as a result of isobaric process, the gas is allowed to expand till its temperature got back to the initial value. Find the total amount of heat absorbed by gas in this process.
View SolutionIf one mole of gas doubles its volume at temperature T isothermally then work done by the gas is
View SolutionA certain mass of a gas is compressed first adiabatically, and then isothermally. In both cases, the initial state of the gas is the same. Is the work done W1 in the first case greater than the work done W2 in the second case ? Explain.
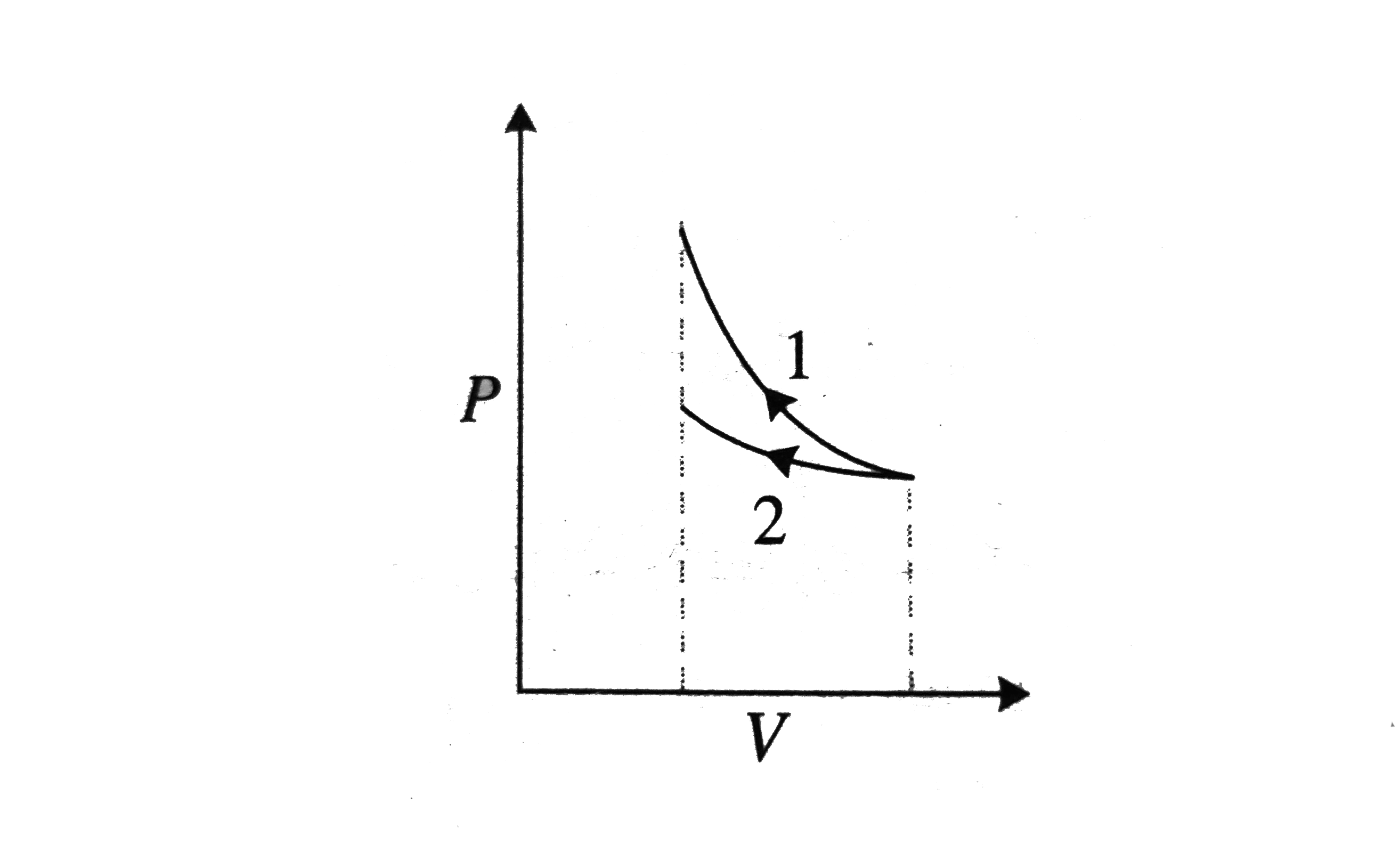
View SolutionVolume versus temperature graph of two moles of helium gas is as shown in figure. The ratio of heat absorbed and the work done by the gas in process 1−2 is
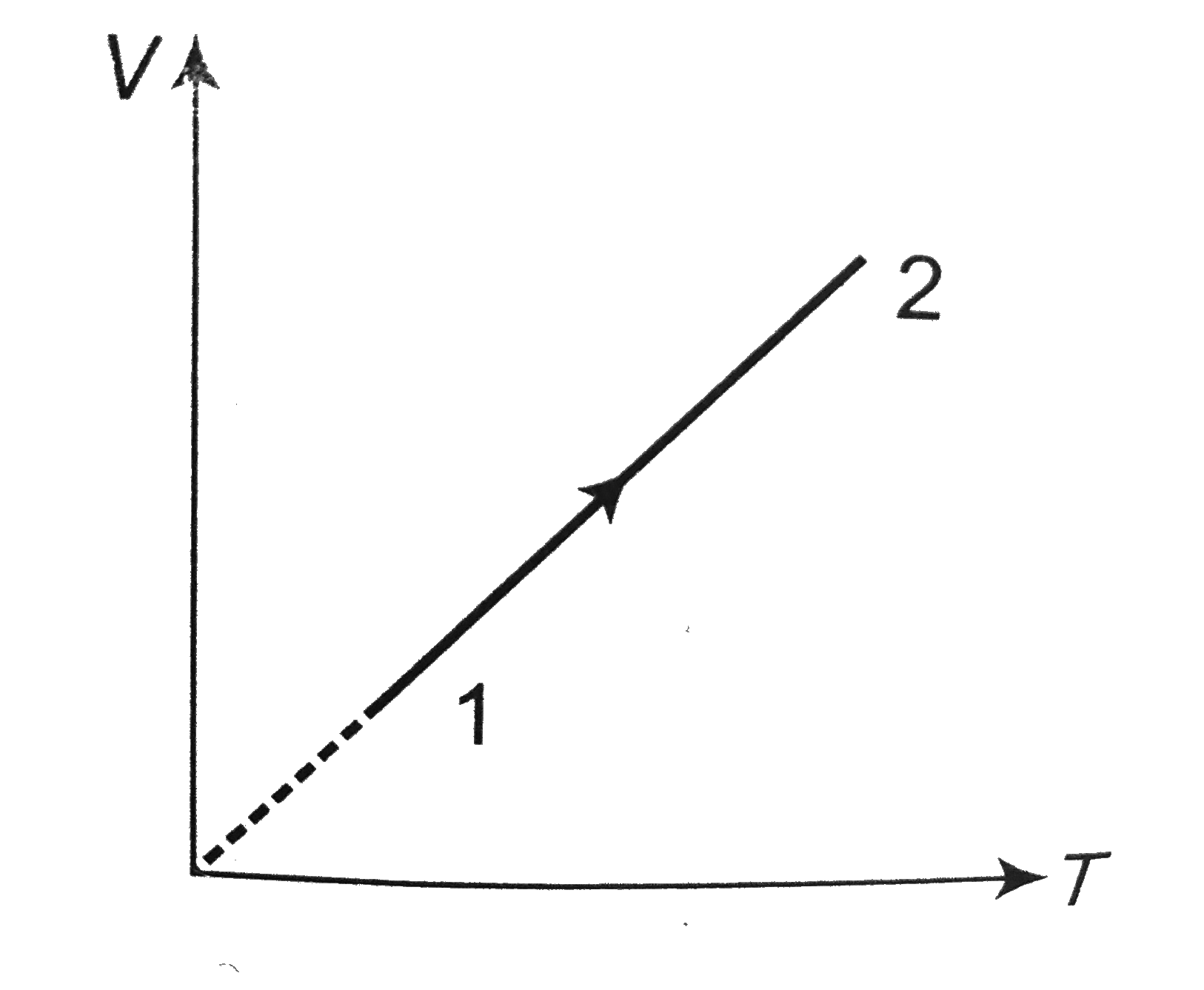
View SolutionVolume versus temperature graph of two moles of helium gas is as shown in figure. The ratio of heat absorbed and the work done by the gas in process 1−2 is

View SolutionSix grams of hydrogen gas at a temperature of 273 K isothoermally expanded to five times its initial volume and then isochorically heated so that the pressure in the final state becomes equal to that in the initial state. Find the total amount of heat absorbed by the gas during the entire process.
View SolutionTwo moles of helium gas(λ=5/3) are initially at temperature 27∘C and occupy a volume of 20 litres. The gas is first expanded at constant pressure until the volume is doubled. Then it undergoes an adiabatic change until the temperature returns to its initial value.
(i) Sketch the process on a p-V diagram.
(ii) What are the final volume and pressure of the gas?
(iii) What is the work done by the gas ?
View SolutionTwo moles of helium gas(λ=5/3) are initially at temperature 27∘C and occupy a volume of 20 litres. The gas is first expanded at constant pressure until the volume is doubled. Then it undergoes an adiabatic change until the temperature returns to its initial value.
(i) Sketch the process on a p-V diagram.
(ii) What are the final volume and pressure of the gas?
(iii) What is the work done by the gas ?
View Solution
