Two moles of an ideal gas at temperature T0=300K was cooled isochorically so that the pressure was reduced to half. Then, in an isobaric process, the gas expanded till its temperature got back to the initial value. Find the total amount of heat absorbed by the gas in the processs
150RJ
300RJ
75RJ
100RJ
The correct Answer is:B
To solve the problem step by step, we will analyze the two processes the gas undergoes: the isochoric cooling and the isobaric expansion.
Step 1: Initial Conditions
We start with 2 moles of an ideal gas at an initial temperature T0=300K.
Step 2: Isochoric Cooling
In the first process, the gas is cooled isochorically (constant volume) until the pressure is halved.
- Let the initial pressure be P0.
- The final pressure after cooling is Pf=P02.
Using the ideal gas law, we can relate the pressures and temperatures:
P0T0=PfTf
Substituting the known values:
P0300=P02Tf
Cross-multiplying gives:
P0Tf=P02⋅300
Cancelling P0 (assuming P0≠0):
Tf=3002=150K
Step 3: Change in Internal Energy (Isochoric Process)
The change in internal energy ΔU1 for an ideal gas during an isochoric process is given by:
ΔU1=nCvΔT
Where ΔT=Tf−T0=150−300=−150K.
Substituting the values:
ΔU1=2Cv(−150)=−300Cv
Since the process is isochoric, the heat absorbed Q1 is equal to the change in internal energy:
Q1=ΔU1=−300Cv
Step 4: Isobaric Expansion
In the second process, the gas expands isobarically (constant pressure) back to the initial temperature T0=300K.
The change in enthalpy ΔH for an ideal gas during an isobaric process is given by:
ΔH=nCpΔT
Where ΔT=T0−Tf=300−150=150K.
Substituting the values:
ΔH=2Cp(150)=300Cp
Since the process is isobaric, the heat absorbed Q2 is equal to the change in enthalpy:
Q2=ΔH=300Cp
Step 5: Total Heat Absorbed
The total heat absorbed by the gas in the entire process is:
Qtotal=Q1+Q2=−300Cv+300Cp
Using the relation Cp−Cv=R:
Qtotal=300(Cp−Cv)=300R
Final Answer
Thus, the total amount of heat absorbed by the gas in the process is:
Qtotal=300RJoules
We start with 2 moles of an ideal gas at an initial temperature T0=300K.
In the first process, the gas is cooled isochorically (constant volume) until the pressure is halved.
- The final pressure after cooling is Pf=P02.
P0T0=PfTf
Substituting the known values:
P0300=P02Tf
Cross-multiplying gives:
P0Tf=P02⋅300
Cancelling P0 (assuming P0≠0):
Tf=3002=150K
The change in internal energy ΔU1 for an ideal gas during an isochoric process is given by:
ΔU1=nCvΔT
Where ΔT=Tf−T0=150−300=−150K.
ΔU1=2Cv(−150)=−300Cv
Q1=ΔU1=−300Cv
In the second process, the gas expands isobarically (constant pressure) back to the initial temperature T0=300K.
ΔH=nCpΔT
Where ΔT=T0−Tf=300−150=150K.
ΔH=2Cp(150)=300Cp
Q2=ΔH=300Cp
The total heat absorbed by the gas in the entire process is:
Qtotal=Q1+Q2=−300Cv+300Cp
Qtotal=300(Cp−Cv)=300R
Thus, the total amount of heat absorbed by the gas in the process is:
Qtotal=300RJoules
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Multiple Corrects
29 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Assertion-Reasoning
6 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Subjective
22 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single correct anwer type
14 Videos
Similar Questions
Two moles of a certain gas at a temperature T0=300K were cooled isochorically so that the pressure of the gas got reduced 2 times. Then as a result of isobaric process, the gas is allowed to expand till its temperature got back to the initial value. Find the total amount of heat absorbed by gas in this process.
View SolutionFour moles of a diatomic gas (g = 1.4) at a temperature of 300 K were cooled isochorically, so that the final pressure was 1/3 times the original pressure. The gas was allowed to expand isobarically till its temperature got back to its original value. Calculate the total amount of heat absorbed during the process. R = 8.31 J mol−1K−1.
View Solution
Knowledge Check
Two moles of an ideal monoatomic gas occupy a volume 2V at temperature 300K, it expands to a volume 4V adiabatically, then the final temperature of gas is
Aa.179 KBb.189 KCc.199 KDd.219 K
Six grams of hydrogen gas at a temperature of 273 K isothoermally expanded to five times its initial volume and then isochorically heated so that the pressure in the final state becomes equal to that in the initial state. Find the total amount of heat absorbed by the gas during the entire process.
View SolutionThree moles of an ideal gas being initially at a temperature Ti=273K were isothermally expanded 5 times its initial volume and then isochorically heated so that the pressure in the final state becomes equal to that in the initial state. The total heat supplied in the process is 80kJ. Find γ(=CpCV) of the gas.
View SolutionAn ideal gas at 300K is expanded isothermally to double its volume,then pressure of the gas will be
View SolutionA fixed mass of a gas is first heated isobarically to double the volume and then cooled isochorically to decrease the temperature back to the initial value. By what factor would the work done by the decreased, had the process been isothermal?
View SolutionTwo moles of an ideal monoatomic gas is taken through a cycle ABCA as shown in the p - T diagram. During the process AB, the pressure and temperature of the gas vary such that pT = constant. If T1=300K and the amount of heat released by the gas during the process AB is Q=−xR, then the value of x is
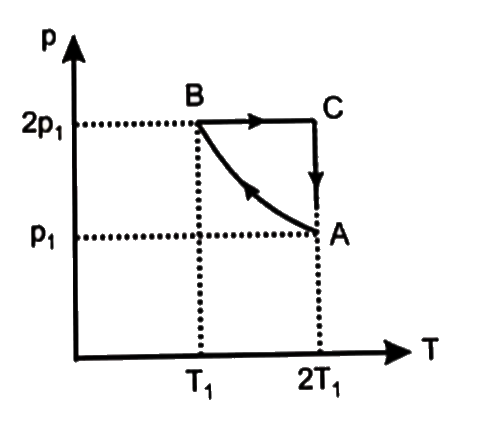
View SolutionIn a flexible balloon 2, moles of SO2 having an initial volume of 1 kL at a temperature of 27.∘C is filled . The gas is first expanded to thrice its initial volume isobarically and then further expanded adiabatically so as to attain its initial temperature . Assuming the gas to be ideal , the work done by the gas in the whole process is [γSO2=43,R=253Jmol−1K−1]
View SolutionTwo moles of an ideal gas was heated isobarically so that its temperature was raised by 100 K. The heat absorbed during the process was 4000 J. Calculate (i) the work done by the gas, (ii) the increase in internal energy and (ii) the value of y for the gas [R=8.31Jmol−1K−1].
View Solution
