A metal ring of initial radius r and cross-sectional area A is fitted onto a wooden disc of radius R > r. If Youngs modules of metal is Y then tension in the ring is
AYRr
AY(R−r)r
YA(R−rr)
YrAR
The correct Answer is:B
As we know Y=FLA×ΔL
F=YA×ΔLL=YA(2πR−2πr)2πr
∴F=YA(R−rr)
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF MATTERBOOK - PHYSICS WALLAHCHAPTER - MECHANICAL PROPERTIES OF MATTEREXERCISE - NEET Past 5 Yeats Questions
16 Videos
- MECHANICAL PROPERTIES OF MATTERBOOK - PHYSICS WALLAHCHAPTER - MECHANICAL PROPERTIES OF MATTEREXERCISE - NEET Past 5 Yeats Questions
16 Videos
- MAGNETISM AND MATTER BOOK - PHYSICS WALLAHCHAPTER - MAGNETISM AND MATTER EXERCISE - NEET PAST 5 YEARS QUESTIONS
10 Videos
- MOTION IN A PLANE BOOK - PHYSICS WALLAHCHAPTER - MOTION IN A PLANE EXERCISE - NEET Past 5 years Questions
10 Videos
Similar Questions
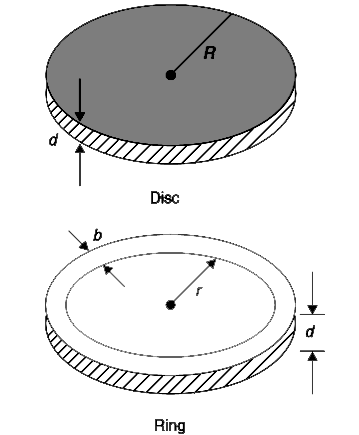
A steel ring is to be fitted on a wooden disc of radius R and thickness d. The inner radius of the ring is r which is slightly smaller than R. The outer radius of the ring is r + b and its thickness is d (same as the disc). There is no change in value of b and d after the ring is fitted over the disc, only the inner radius becomes R. If the Young’s modulus of steel is Y, calculate the longitudinal stress developed in it. Also calculate the tension force developed in the ring.
[Take b<<r]
View SolutionA uniform ring of radius R and made up of a wire of cross - sectional radius r is rotated about its axis with a frequency f. If density of the wire is ρ and young's modulus is Y . Find the fractional change in radius of the ring .
View Solution
Knowledge Check
A metal ring of initial radius r and cross-sectional area A is fitted onto a wooden disc of radius R > r. If Youngs modules of metal is Y then tension in the ring is
AAYRrBAY(R−r)rCYA(R−rr)DYrARA steel ring of radius r and cross section area A is fitted on to a wooden disc of radius R(R>r). If Young's modulus be E, then the force with which the steel ring is expanded is
AAERrBAE(R−rr)CEA(R−rA)DErARA metallic rod of radius 2cm and cross sectional area 4cm2 is fitted into a wooden circular disc of radisu 4cm. If the Young's modulus of the materail of the ring is 2×1011N/m2, the force with which the metal ring expands is:
A2×107NB8×107NC4×107ND6×107N
A ring of radius R is having charge Q uniformly distributed. A point charge Q0 is placed at the centre of the ring. Find tension developed in the ring. If radius of cross - section of the ring is a and Young's modulus of wire is Y, find increase in the radius of ring.
View SolutionA metal rign of mass m and radius R is placed on a smooth horizontal table and is set rotating abut its own axis in such a way that each part of the ring moves with a speed v. Find the tension in the ring.
View SolutionA circular tube of radius R and across- sectional radius r(r<<R) is filled completely with iron balls of th radius ρ. Iron balls just fitting into the tube . The tension in the tube when it is rotated about its axis perpendicular to its plane with angular velocity ω
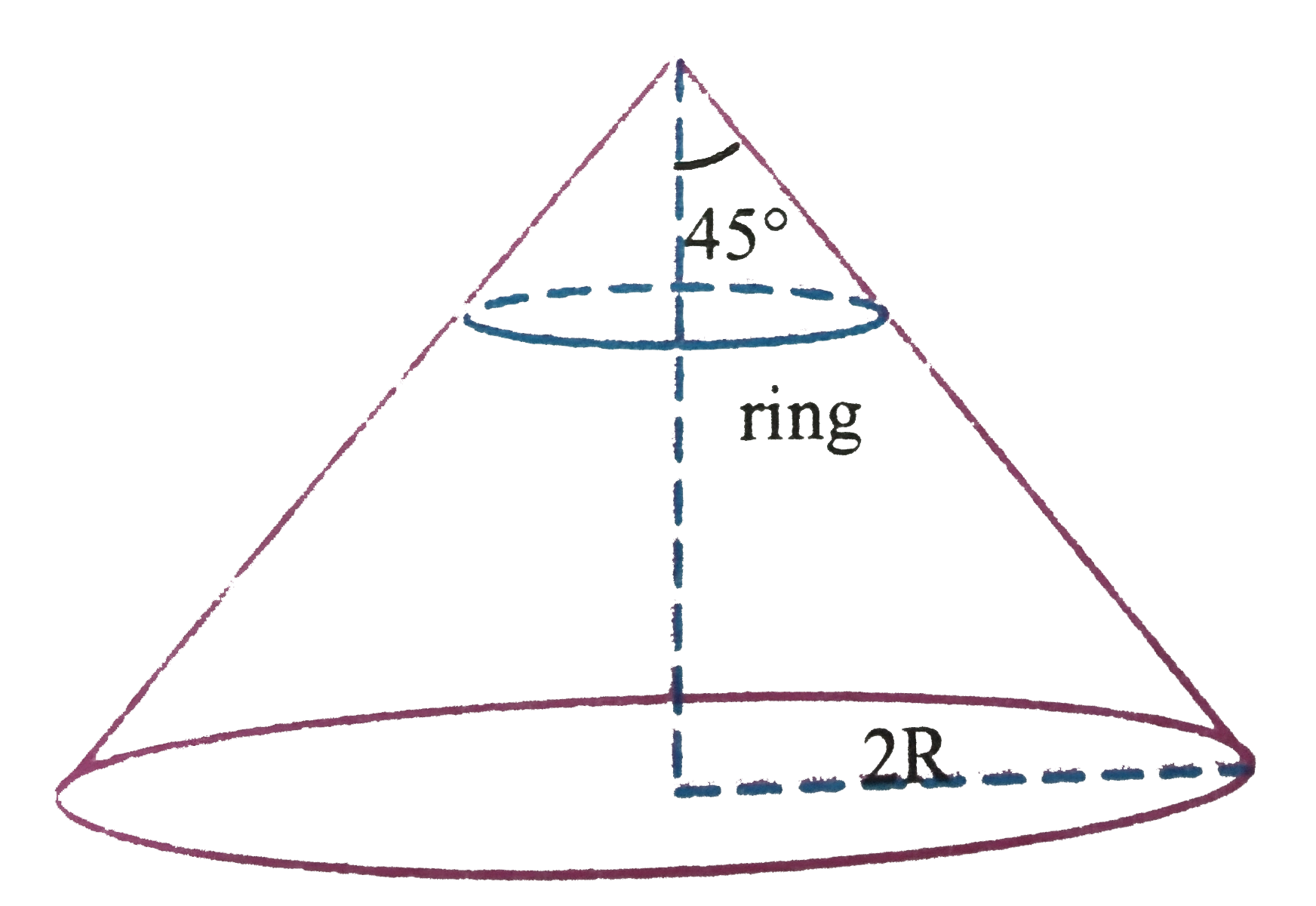
View SolutionA unifrom metallic ring of mass m, radisus R, cross sectional area 'a' and young'/s modulus Y kis kept on a smooth cone of radius 2R and semivertex angle 45∘ as shown. [Assume that extension in the ring is small]
View SolutionCharges q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
View Solution
