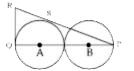
In the given figure. Two identical circles of radius 4 cm touch each other. A and B are the centres of the two circles. If RQ is a tangent to the circle, then what is the length (in cm) of RQ?
3√3
2√6
4√2
6√2
Step by step video & image solution for In the given figure. Two identical circles of radius 4 cm touch each other. A and B are the centres of the two circles. If RQ is a tangent to the circle, then what is the length (in cm) of RQ? by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
In the given figure. Two identical circles of radius 4 cm touch each other. A and B are the centres of the two circles. If RQ is a tangent to the circle, then what is the length (in cm) of RQ?
 A3√3B2√6C4√2D6√2
A3√3B2√6C4√2D6√2Two circles of radii 8 cm and 6 cm touch each other externally. The length of the direct common tangent is:
8 सेमी तथा 6 सेमी त्रिज्याओं वाले दो वृत्त एक-दूसरे को बाहर से स्पर्श करते हैं | प्रत्यक्ष उभयनिष्ठ स्पर्श रेखा की लंबाई कितनी है ?A20B24C13.86D10.12There are two identical circles of radius 10 cm each. If the length of the direct common tangent is 26 cm, then what is the length (in cm) of the transverse common tangent?
A2√69B4√23C4√46D3√46
If two circles of radius 4cm and 1cm touch each other externally then length of the direct common tangents is
View SolutionThere are two identical circles of radius 10 cm each. If the length of the direct common tangent is 26 cm, then what is the length (in cm) of the transverse common tangent?
View SolutionDraw two circle of radius 5 cm and 3 cm with their centres 9 cm apart. From the centre of each circle, draw tangents to other circles.
View SolutionTwo concentric circles with radius 3 cm and 9.25 cm. Find the length of the chord of the bigger circle which is tangent to the other circle.
View SolutionThe length of the tangent drawn to a circle of radius 4 cm from a point 5 cm away from the centre of the circle is
View Solution
