Question

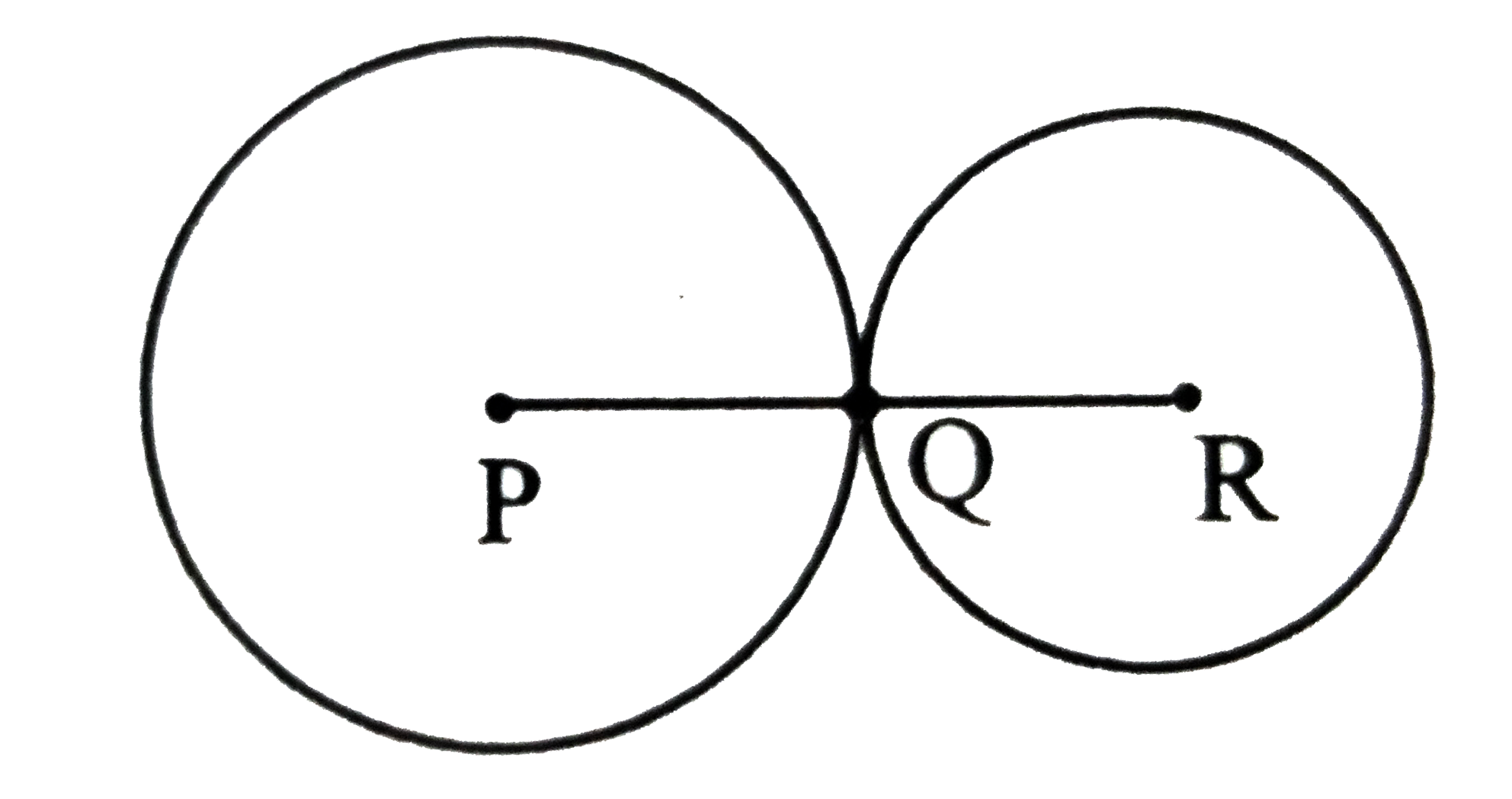
Two circles of radius 5 cm and 4 cm touch each other. Find the distance between their centers.

Answer

9 cm or 1 cm

Explanation

To solve the problem of finding the distance between the centers of two circles that touch each other, we will follow these steps:

Step 1: Understand the Problem
We have two circles with given radii:
- Radius of the first circle (R1) = 5 cm
- Radius of the second circle (R2) = 4 cm

The circles are touching each other. We need to determine the distance between their centers.

Step 2: Identify the Type of Touching
Since the problem states that the circles touch each other, we need to consider two scenarios:
1. Externally touching circles: The distance between their centers is the sum of their radii.
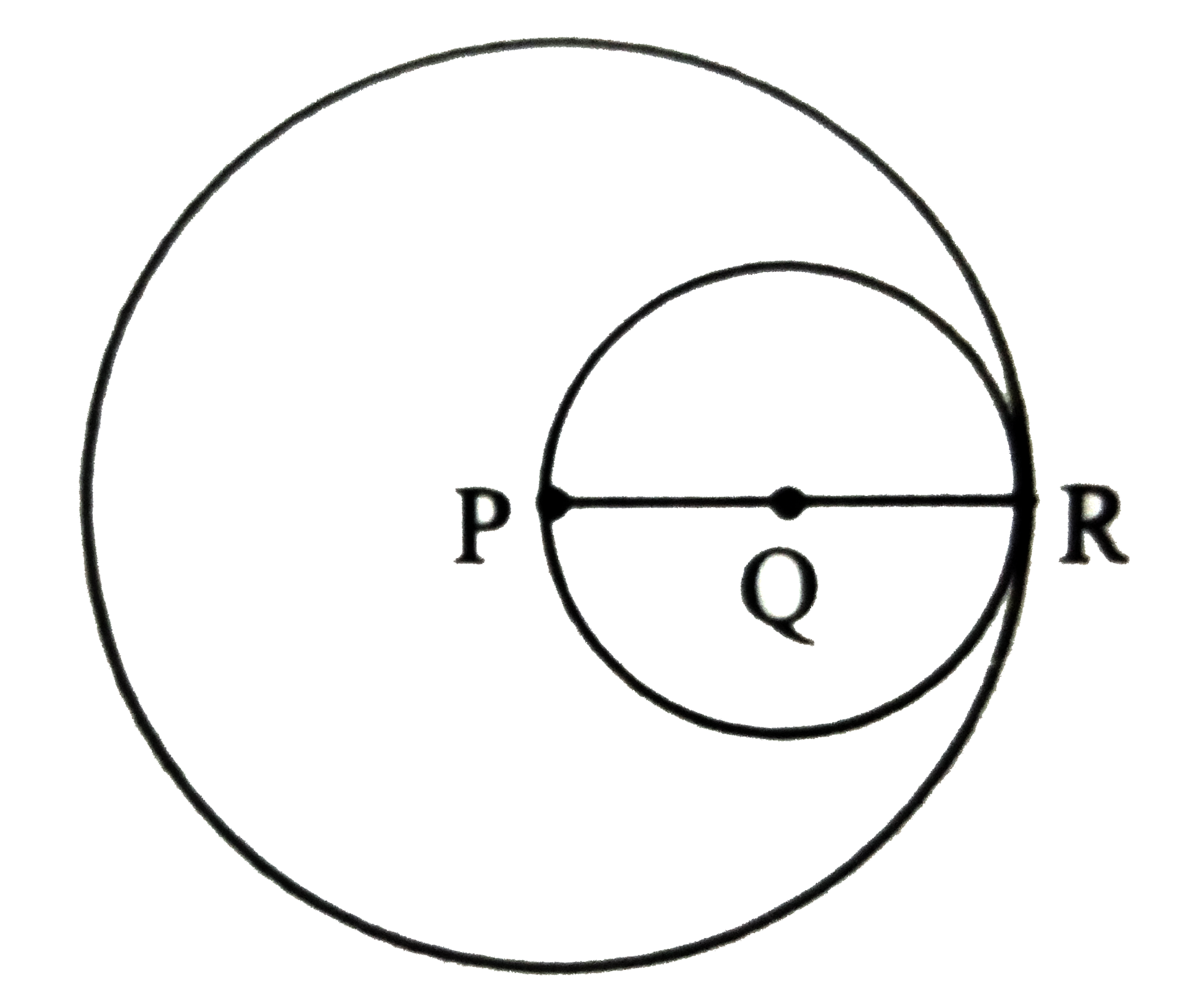
2. Internally touching circles: The distance between their centers is the difference of their radii.

Step 3: Calculate the Distance for Externally Touching Circles
If the circles are touching each other externally, the formula for the distance \( D \) between their centers is:
\( D = R1 + R2 \)

Substituting the values:
\( D = 5 \, \text{cm} + 4 \, \text{cm} = 9 \, \text{cm} \)

Step 4: Calculate the Distance for Internally Touching Circles
If the circles are touching each other internally, the formula for the distance \( D \) between their centers is:
\( D = R1 - R2 \)

Substituting the values:
\( D = 5 \, \text{cm} - 4 \, \text{cm} = 1 \, \text{cm} \)

Conclusion
The distance between the centers of the two circles depends on how they are touching:
- If they are touching externally, the distance is 9 cm.
- If they are touching internally, the distance is 1 cm.