There is a box of cuboid shape. The smallest side of box is 20 cm and largest side is 40 cm. Which of the following can be volume (in cm3) of the box?
घनाभ आकार का शक बक्सा है। बक्से की सबसे छोटी भुजा 20 से.मी. तथा सबसे बड़ी भुजा 40 से.मी. है। निम्नलिखित मे से बक्से का आयतन (से.मी.^3 में) क्या हो सकता है?
18000
12000
36000
42000
To find the possible volume of a cuboid-shaped box given the dimensions, we can follow these steps:
Step 1: Identify the dimensions of the cuboid
We know that the smallest side of the box is 20 cm and the largest side is 40 cm. Let's denote:
- Length (L) = 40 cm (largest side)
- Breadth (B) = 20 cm (smallest side)
- Height (H) = x cm (the third side, which can vary)
Step 2: Determine the range for the third side
Since the third side (H) must be between the smallest and largest sides, we have:
- 20 cm < H < 40 cm
Step 3: Write the formula for the volume of the cuboid
The volume (V) of a cuboid is given by the formula:
V=L×B×H
Substituting the known values:
V=40×20×x
V=800x
Step 4: Determine the range for the volume
Now, we need to find the range of possible volumes by substituting the limits for x:
- Minimum volume when H=20:
Vmin=800×20=16000cm3
- Maximum volume when H=40:
Vmax=800×40=32000cm3
Thus, the volume of the box can range from 16000 cm³ to 32000 cm³.
Step 5: Evaluate the given options
Now we need to check which of the provided options fall within the range of 16000 cm³ to 32000 cm³.
1. Option 1: 18000 cm³ - This is within the range.
2. Option 2: 12000 cm³ - This is below the range.
3. Option 3: 36000 cm³ - This is above the range.
4. Option 4: 37000 cm³ - This is also above the range.
Conclusion
The only possible volume of the box from the given options is 18000 cm³.
---
We know that the smallest side of the box is 20 cm and the largest side is 40 cm. Let's denote:
- Length (L) = 40 cm (largest side)
- Breadth (B) = 20 cm (smallest side)
- Height (H) = x cm (the third side, which can vary)
Since the third side (H) must be between the smallest and largest sides, we have:
- 20 cm < H < 40 cm
The volume (V) of a cuboid is given by the formula:
V=L×B×H
Substituting the known values:
V=40×20×x
V=800x
Now, we need to find the range of possible volumes by substituting the limits for x:
- Minimum volume when H=20:
Vmin=800×20=16000cm3
- Maximum volume when H=40:
Vmax=800×40=32000cm3
Now we need to check which of the provided options fall within the range of 16000 cm³ to 32000 cm³.
2. Option 2: 12000 cm³ - This is below the range.
3. Option 3: 36000 cm³ - This is above the range.
4. Option 4: 37000 cm³ - This is also above the range.
The only possible volume of the box from the given options is 18000 cm³.
Topper's Solved these Questions
Similar Questions
A regular hexagonal base prism has height 8 cm and side of base is 4cm. What is the total surface area (in cm2) of the prism?
एक सम षट्भुज आधार वाले प्रिज्म की ऊँचाई 8 से.मी. है तथा आधार को भुजा 4 से.मी. है। प्रिज्म का कुल पृष्ठीय क्षेत्रफल (से.मी.2 में) क्या है?
View SolutionA right triangular prism has equilateral triangle as its base. Side of the triangle is 15 cm. Height of the prism is 20√3 cm. What is the volume (in cm3) of the prism?
एक लम्बवत त्रिभुजाकार प्रिज्म का आधार समबाहु त्रिभुज है। त्रिभुज को भुजा 15 से.मी. है। प्रिज्म की ऊँचाई 20√3से.मी. है। प्रिज्म का आयतन (से.मी.2 में) क्या है?
View SolutionThe base of a prism is in the shape of an equilateral triangle. If the perimeter of the base is 18 cm and the height of the prism is 20 cm, then what is the volume (in cm3) of the prism?
एक प्रिज्म का आधार समबाहु त्रिभुज के आकार में है। यदि आधार की परिधि 18 से.मी. है तथा प्रिज्म को ऊँचाई 20 से.मी. है, तो प्रिज्म का आयतन (से.मी.3 में) क्या हैं?
View SolutionThe height of a cone is 24 cm and the area of the base is 154 cm2. What is the curved surface area (in cm2) of the cone?
एक शंकु की ऊँचाई 24 से.मी. है तथा आधार का क्षेत्रफल 154 से.मी.2 है। शंकु के वक्र पृष्ठिय क्षेत्रफल (से.मी.2 में) क्या है?
View SolutionA pyramid has a square base, whose side is 8 cm. If the height of pyramid is 16 cm, then what is the total surface area (in cm2) of the pyramid?
एक पिरामिड का आधार वर्ग है जिसकी भुजा 8 से.मी. है। यदि पिरामिड की ऊँचाई 16 से.मी. है, तो पिरामिड का कूल पृष्ठिय क्षेत्रफल (से.मी.2 में)क्या हैं।
View SolutionA regular pyramid has a square base. The height of the pyramid is 22 cm and side of its base is 14 cm. Volume of pyramid is equal to the volume of a sphere. What is the radius (in cm) of the sphere?
एक सम पिरामिड का आधार एक वर्ग है। पिरामिड को ऊँचाई 22 से.मी. है तथा उसके आधार की भुजा 14 से.मी. है। पिरामिड का आयतन एक गोले के आयतन के बराबर हैं गोले की त्रिज्या (से.मी. में) क्या है?
View SolutionTwo spheres of equal radius are taken out by cutting from a solid cube of side (12+4√3) cm. What is the maximum volume (in cm3) of each sphere?
समान त्रिज्या वाले दो गोले को एक ठोस घन जिसकी भुजा (12+4√3) से.मी. है, से काट कर निकाला गया है।, प्रत्येक गोले का अधि कतम आयतन (से.मी.3 में) क्या है?
View SolutionA pyramid has a square base. The side of square is 12 cm and height of pyramid is 21 cm. The pyramid is cut into 3 parts by 2 cuts parallel to its base. The cuts are at height of 7 cm and 14 cm respectively from the base. What is the difference (in cm3) in the volume of top most and bottom most part?
एक पिरामिड का आधार एक वर्ग है। वर्ग की भुजा 12 से.मी. तथा पिसमिड की ऊँचाई 21 से.मी. है। पिरामिड को उसके आधार के समांतर 2 कर्टावों से 3 भागों में काटा जाता है। कटाव आधार से. क्रमशः 7 से.मी. तथा 14 से.मी. को ऊँचाई पर है। सबसे ऊपर तथा सबसे नीचे के भाग के आयतन का अंतर (से.मी.3 में)क्या हैं।
View SolutionIn the given figure, PQR is an equilateral triangle with side as 12cm. S and T are the mid points of the sides PQ and PR respectively. What is the area (in cm2) of the shaded region?
दी गई आकृति में PQR एक समबाहु त्रिभुज है जिसकी भुजा 12 से.मी. हैं। S तथा T क्रमशः भुजा PQ तथा PR के मध्य बिन्दु है। छायांकित भाग का क्षेत्रफल (से.मी.2 में) क्या है?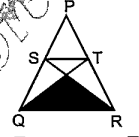
View SolutionIn the given figure, ABCD and BEFG are squares of sides 8 cm and 6 cm respectively. What is the area (in cm2) of the shaded region?
दी गई आकृति में, ABCD तथा BEFG क्रमश: 8 से.मी. तथा 6 से.मी. भुजा वाले वर्ग हैं। आच्छादित भाग का क्षेत्रफल (से.मी.2 में) क्या हैं?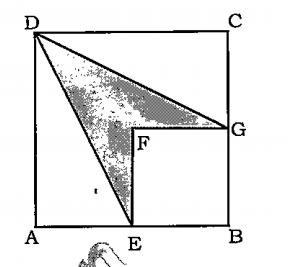
View Solution
