PA and PB are two tangents drawn to two cricles of radius 3 cm and 5 cm respectively. PA touches the smaller and larger circles at points X and Y respectively. PB touches the smaller and large circle at point U and V respectively. The centres of the smaller and larger circles are O and N respectively. If ON=12 cm, then what is the value (in cm) of PY?
PA तथा PB क्रमश, 3 सेमी. तथा 5 सेमी. वाले दो वृत्तों पर स्पर्श रेखाएँ बनाई गई है। PA छोटे तथा बड़े वृत्त को क्रमशः X तथा Y बिन्दु पर स्पर्श करते है। PB छोटे तथा बड़े वृत्त को U तथा V बिंदु पर स्पर्श करती है। O तथा N क्रमश: छोटे तथा बड़े वृत्त के केन्द्र हैं। यदि
ON=12 सेमी. है, तो PY का मान (सेमी. में) क्या है?
5√35
7√15
9√15
12√5
To solve the problem step by step, we will follow the reasoning outlined in the video transcript.
Step 1: Understand the Setup
We have two circles:
- A smaller circle with radius r1=3 cm and center O.
- A larger circle with radius r2=5 cm and center N.
The distance between the centers O and N is given as ON=12 cm.
Step 2: Identify the Tangents
Let:
- PA be the tangent to the smaller circle at point X and to the larger circle at point Y.
- PB be the tangent to the smaller circle at point U and to the larger circle at point V.
Step 3: Analyze the Triangles
We can form two right triangles:
1. Triangle POX where PX is the tangent from point P to point X on the smaller circle.
2. Triangle PYB where PY is the tangent from point P to point Y on the larger circle.
Step 4: Use the Properties of Right Triangles
Since both PA and PB are tangents to the circles, we know:
- ∠OXP=90∘
- ∠NYP=90∘
This means triangles POX and PYB are similar by AA similarity (Angle-Angle).
Step 5: Set Up the Ratios
From the similarity of triangles, we have:
NYOX=PNPO
Where:
- NY=r2=5 cm (radius of the larger circle)
- OX=r1=3 cm (radius of the smaller circle)
Step 6: Express PN in Terms of PO
Let PO=x. Then, since ON=12 cm:
PN=PO+ON=x+12
Substituting this into the ratio gives:
53=x+12x
Step 7: Cross-Multiply and Solve for x
Cross-multiplying gives:
5x=3(x+12)
Expanding and simplifying:
5x=3x+365x−3x=362x=36x=18
Thus, PO=18 cm.
Step 8: Calculate PN
Now substituting back to find PN:
PN=PO+ON=18+12=30 cm
Step 9: Use Pythagorean Theorem to Find PY
In triangle PYN:
PN2=PY2+NY2
Substituting the known values:
302=PY2+52900=PY2+25PY2=900−25PY2=875PY=√875=5√35 cm
Final Answer
Thus, the value of PY is 5√35 cm.
We have two circles:
- A smaller circle with radius r1=3 cm and center O.
- A larger circle with radius r2=5 cm and center N.
The distance between the centers O and N is given as ON=12 cm.
Let:
- PA be the tangent to the smaller circle at point X and to the larger circle at point Y.
- PB be the tangent to the smaller circle at point U and to the larger circle at point V.
We can form two right triangles:
1. Triangle POX where PX is the tangent from point P to point X on the smaller circle.
2. Triangle PYB where PY is the tangent from point P to point Y on the larger circle.
Since both PA and PB are tangents to the circles, we know:
- ∠OXP=90∘
- ∠NYP=90∘
From the similarity of triangles, we have:
NYOX=PNPO
Where:
- NY=r2=5 cm (radius of the larger circle)
- OX=r1=3 cm (radius of the smaller circle)
Let PO=x. Then, since ON=12 cm:
PN=PO+ON=x+12
Substituting this into the ratio gives:
53=x+12x
Cross-multiplying gives:
5x=3(x+12)
Expanding and simplifying:
5x=3x+365x−3x=362x=36x=18
Thus, PO=18 cm.
Now substituting back to find PN:
PN=PO+ON=18+12=30 cm
In triangle PYN:
PN2=PY2+NY2
Substituting the known values:
302=PY2+52900=PY2+25PY2=900−25PY2=875PY=√875=5√35 cm
Thus, the value of PY is 5√35 cm.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Two circles of radii 8 cm and 2 cm respectively touch each other externally at the point A. PQ is the direct common tangent of these two circles of centres O1andO2 respectively. The length of PQ is equal to :
A4 cmB8 cmC2 cmD3 cmIf two circles with radii 5 cm and 3 cm respectively touch externally, then the distance between their centre is ________
A2cmB4cmC8cmD16cm
Two circles with radius 4 cm and 9 cm respectively touch each other externally. Their common tangent touches the circles at point P and Point Q respectively. Then, area of the square with side PQ is.
View SolutionTwo concentric circles are of radii 7cm and rcm respectively, where r>7. A chord of the larger circle of length 46cm, touches the smaller circle. Find the value of r.
View SolutionPA and PB are tangents to the circle with centre O touching it at A and B respectively. IF ∠APO=25∘ , then ∠POB is
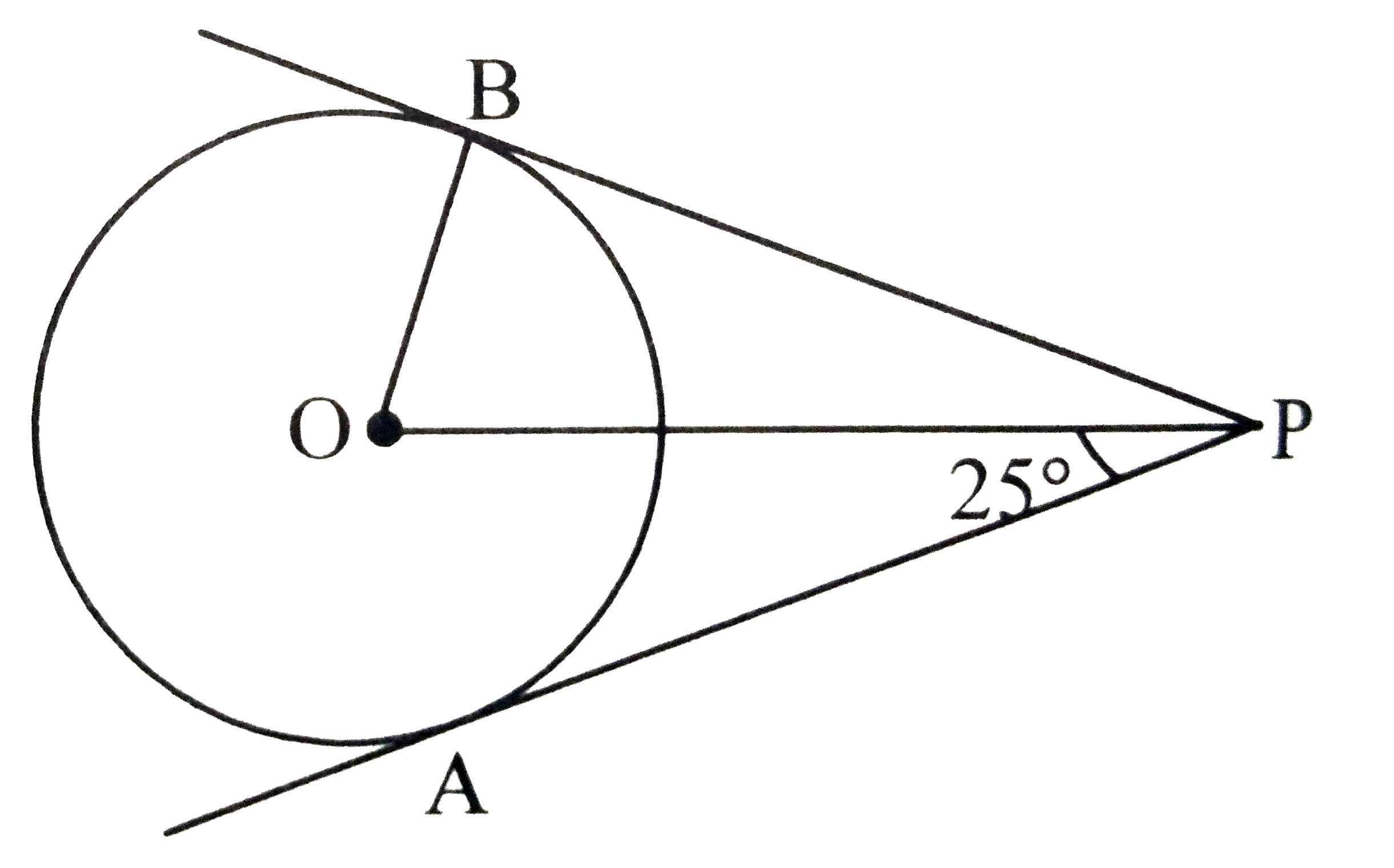
View SolutionPA and PB are the two tangents drawn on a circle from and external point P. The centre of the circle is O and the tangents touches the circles at points A and B. Then quadrilateral OAPB is-
View SolutionDraw two concentric circles of radii 3 cm and 5 cm. Construct a tangent to the smaller circle from a point on the larger circle. Also, measure its length.
View SolutionDraw two concentric circles of radii 3 cm and 5 cm . Construct a tangent to smaller circle from a point on the larger circle . Also measure its length.
View Solution