AB is the diameter of a circle and AC is its chord such that ∠BAC = 30∘. If the tangent at C intersects AB extended at D, then BC = BD.
Step by step video & image solution for AB is the diameter of a circle and AC is its chord such that angle BAC = 30^@. If the tangent at C intersects AB extended at D, then BC = BD. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB=50∘. If AT is the tangent to the circle at the point A, then ∠BAT is equal to
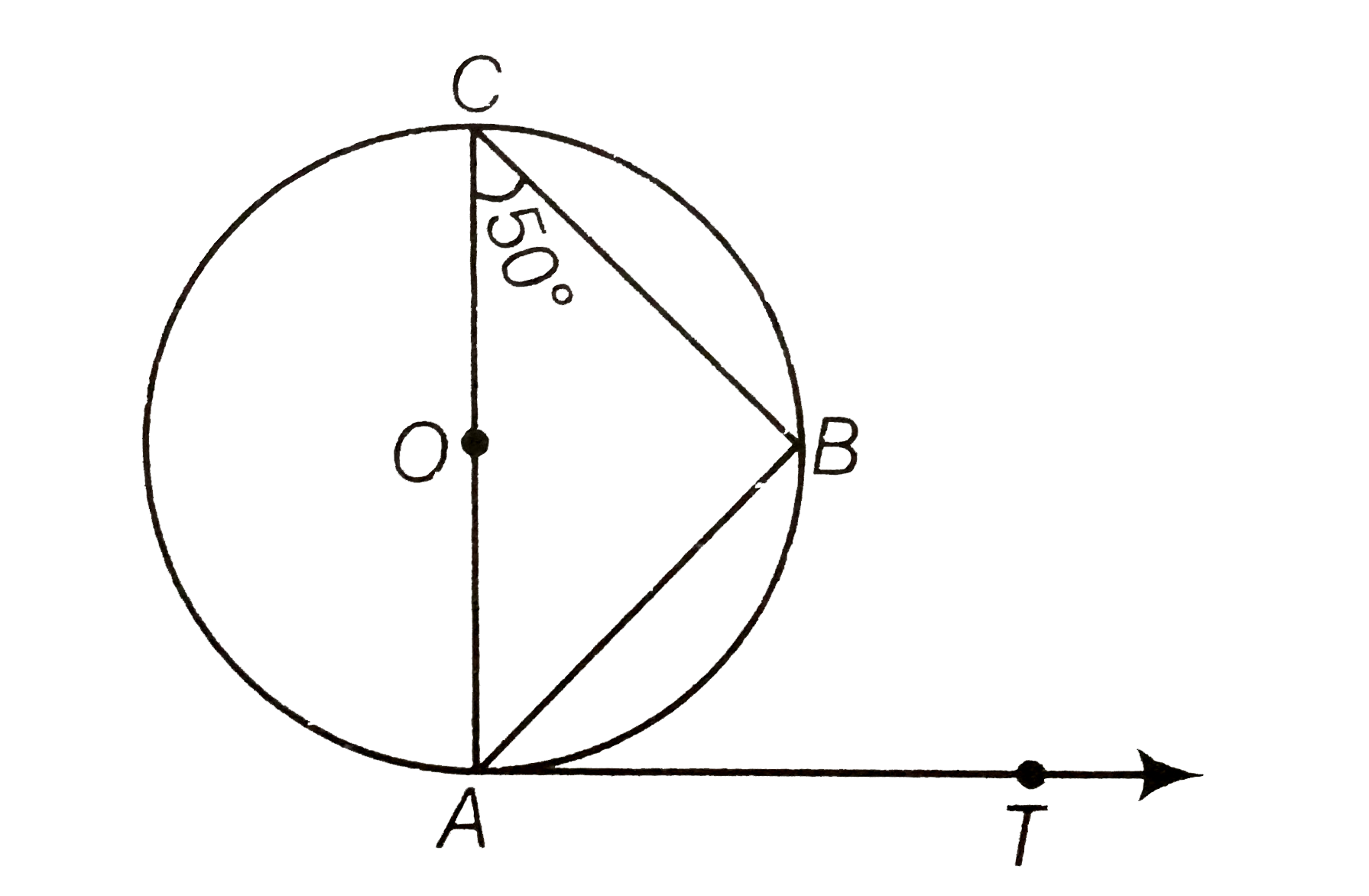 A45∘B60∘C50∘D55∘
A45∘B60∘C50∘D55∘ - Question 2 - Select One
In a circle with the centre is O and AB is the diameter of the circle and CD is the chord of the circle. If angle ABC is 54∘ and the length of CD and BC is equal, then find the ∠DBC.
A1. 36∘B2. 24∘C3. 48∘D4. 12∘ - Question 3 - Select One
AD is a diameter of a circle and AB is a chord. If AD = 34cm, AB = 30cm, the distance of AB form the centre of the circle is
A17 cmB15 cmC4 cmD8 cm
AB is a diameter of a circle. CD is a chord parallel to AB and 2CD = AB. The tangent at B meets the line AC produced at E then AE is equal to
View SolutionAD is the diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is
View SolutionSeg AB is a diameter of a circle with centre P. Seg AC is a chord. A secant through P and parallel to seg AC intersects the tangent drawn at C in D. Prove that line DB is a tangent to the circle.
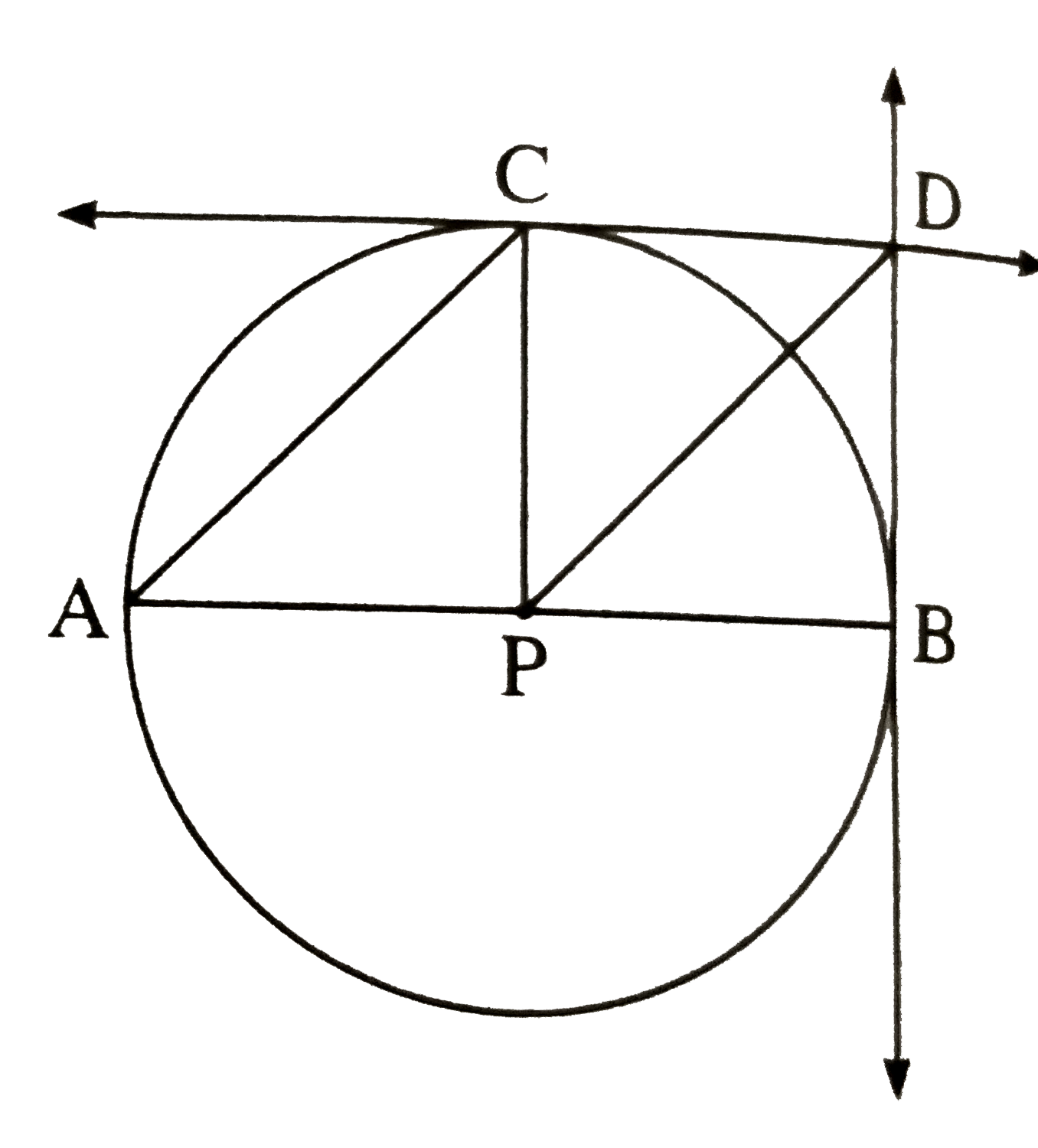 View Solution
View SolutionIn Fig. 10.32, AB is a diameter of the circle, CD is a chord equal to theradius of the circle. AC and BD when extended intersect at a point E. Prove that∠AEB = 60∘
View SolutionAB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Find the ∠AEB.
View Solution

