If a circle touches the side BC of a triangle ABC at P and extended sides AB and AC at Q and R respectively, prove that AQ = 12(BC+CA+AB).
Step by step video solution for If a circle touches the side BC of a triangle ABC at P and extended sides AB and AC at Q and R respectively, prove that AQ = 1/2 (BC + CA + AB). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
Similar Questions
A circle touches the side BC of ΔABC at P and touches AB and AC produced at Q and R respectively. Prove that AQ=1/2(Perimeter of ΔABC).
View SolutionA circle is touching the side BC of a △ABC at point P and touching AB and AC produced at Q and R respectively. Prove that AQ=12(perimeter of △ABC).
View Solution
Knowledge Check
- Question 1 - Select One
In the figure shown here, a circle touches the side BC of a triangle ABC at P and AB and AC produced at Q and R respectively. What is AQ equal to ?
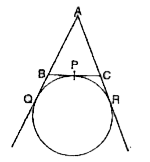 AOne-third of the perimeter of Δ ABC.BHalf of the perimeter of Δ ABC.CTwo-third of the perimeter of Δ ABCDThree-fourth of the perimeter of Δ ABC
AOne-third of the perimeter of Δ ABC.BHalf of the perimeter of Δ ABC.CTwo-third of the perimeter of Δ ABCDThree-fourth of the perimeter of Δ ABC - Question 2 - Select One
A circle touches the side BC of a ΔABC at P and also touches AB and AC produced at Q and R, respectively. If the perimeter of ΔABC = 26.4 cm, then the length of AQ is:
A8.8 cmB13.2 cmC15.4 cmD17.6 cm - Question 3 - Select One
In triangle ABC , sides AB and AC are extended to D and E, respectively, such that AB=BD and AC =CE,F∈dDE,ifBC=6 cm.
A3 cmB6cmC9 cmD12 cm
A circle is touching the side BC of ABC at P and touching AB and AC produced at Q and R respectively. Prove that AQ=12(Perimeter of ABC) .
View SolutionA circle is touching the side BC of ΔABC at P and touching AB and AC produced at Q and R respectively Prove that AQ=12(Perimeter of ΔABC)
View Solution
If a circle touches the side BC at point P, extended side AB at Q and extended side AC at R. Then AQ is equal to :View SolutionA circle touches the side BC of ΔABC at F and touches AB and AC at D and E, respectively. If AD = 8 cm, then find the perimeter of ΔABC.
 View Solution
View SolutionThe incircle of an isoceles triangle ABC, with AB=AC, touches the sides AB,BC and CA at D,E and F respecrively. Prove that E bisects BC.
View Solution

