A chord PQ of a circle is parallel to the tangent drawn at a point R of the circle. Prove that R bisector the arc PRQ.
Step by step video & image solution for A chord PQ of a circle is parallel to the tangent drawn at a point R of the circle. Prove that R bisector the arc PRQ. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A circle with radius r has a chord PQ whose length is 2a. The tangents drawn at points PandQ to the circle meet at T, what is the length of TP?
Aar√r2−a2B2ar√r2−a2Cr2+a2√r2−a2Darr−a - Question 2 - Select One
If the length of a chord of a circle , which makes a angle 45∘ with the tangent drawn at one end point of the chord , is 6 cm , then the radius of the circle is :
A6√2 cmB5 cmC3√2 cmD6 cm - Question 3 - Select One
A chord of a circle is equal to its radius. A tangent is drawn to the circle at an extremity of the chord. The angle between the tangent and the chord is
A30∘B45∘C60∘D75∘
From a point P outside a circle with centre O, tangents PA and PB are drawn to the circle. Prove that OP is the right bisector of the line segment AB.
View SolutionProve that the tangents drawn at the end points of a chord of a circle make equal angles with the chord.
View SolutionProve that the length of the tangents drawn from an external point to a circle are equal.
View SolutionSeg AB is a diameter of a circle with centre P. Seg AC is a chord. A secant through P and parallel to seg AC intersects the tangent drawn at C in D. Prove that line DB is a tangent to the circle.
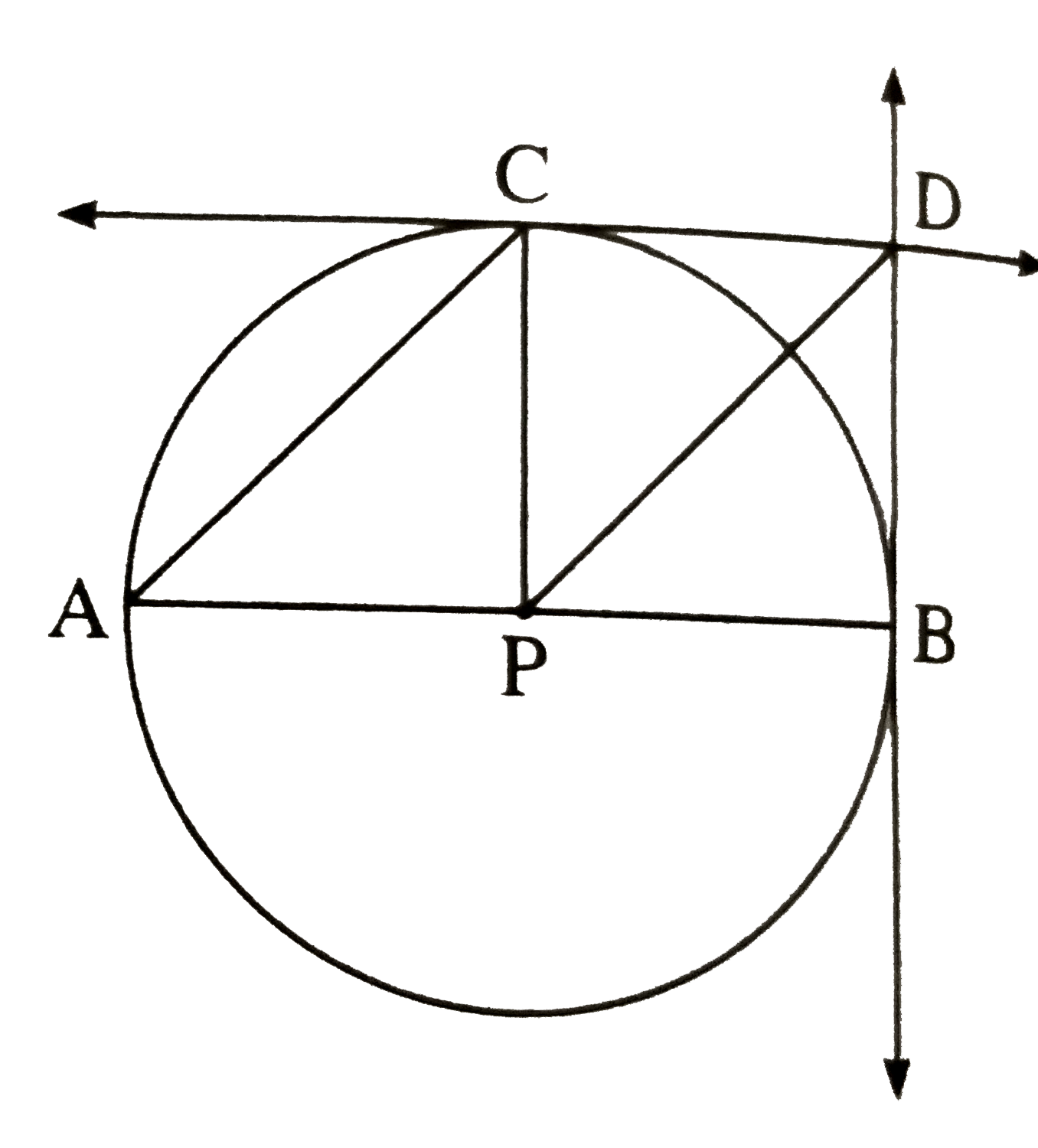 View Solution
View SolutionTangents are drawn at extremities AB of a diameter of a circle centred at P. If tangents drawn at a point C on the circle meet the other two tangents respectively at Q and R then measure of ∠QPR is
View Solution

