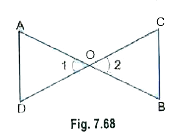In the figure.If OAOD=OCOB, then

which pair of angle are equal?
Step by step video & image solution for In the figure.If ("OA")/("OD")=("OC")/("OB"), then which pair of angle are equal? by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
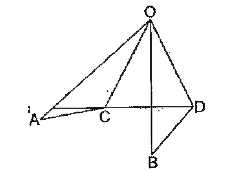
OA, OB, OC are the sides of a rectangular parallelopiped whose diagonals are OO', AA' , BB' and CC' . D is the centre of the rectangle AC'O'B' and D' is the centre of the rectangle O'A'CB' . If the sides OA, OB , OC are in the ratio 1:2:3 , the angle∠DOD' is equal to
Acos−1(24)√697Bcos−1(22)√619Csin−1(24)√697Dsin−1(22)√619In the given figure, OA = OB, OC = OD, ∠AOB=∠COD. Which of the following statements is true?
 AAC = CDBOA=ODCAC=BDD∠OCA=∠ODC
AAC = CDBOA=ODCAC=BDD∠OCA=∠ODC
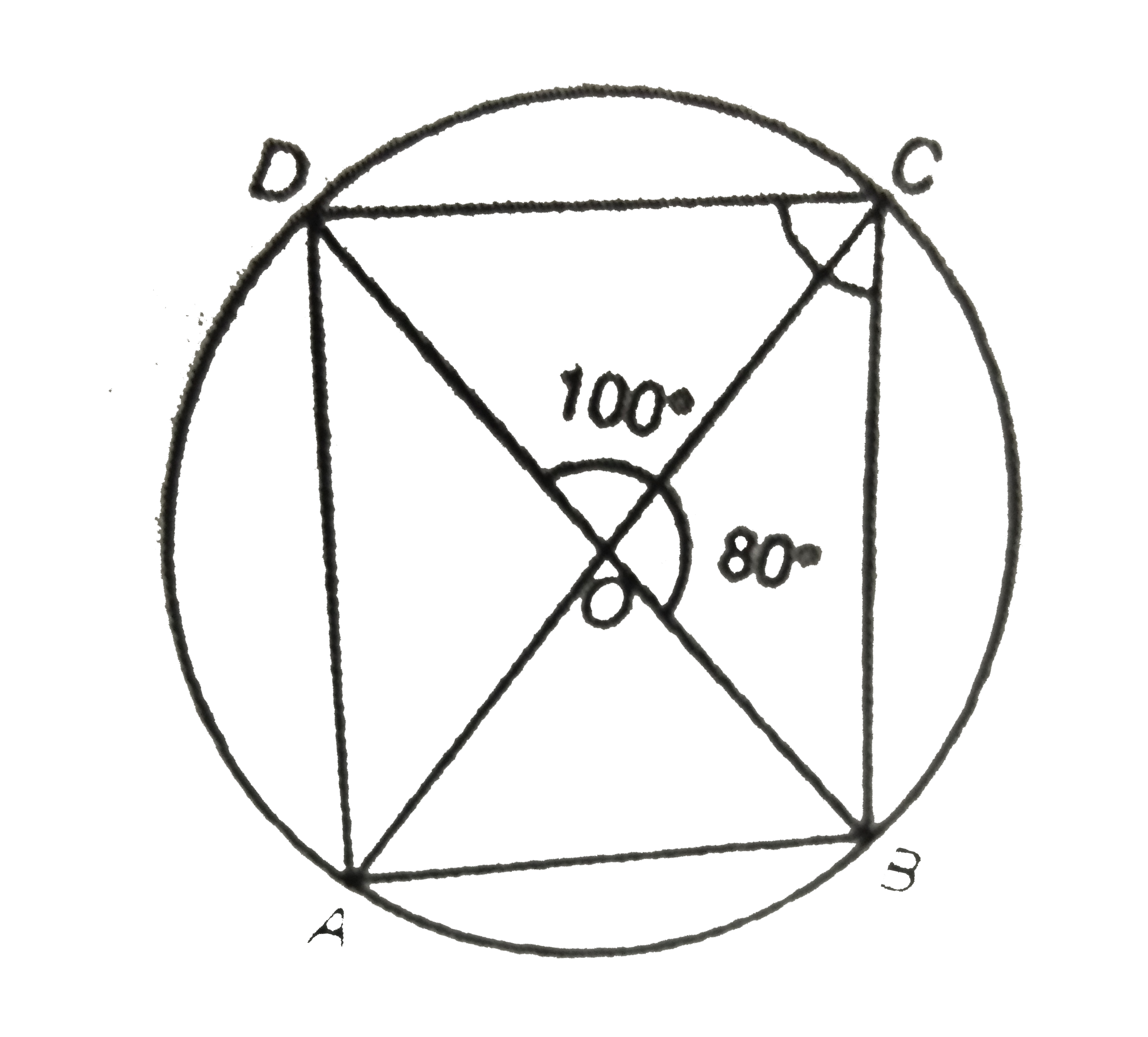
In the given figure, OC.OD = OA.OB
Show that : ∠A=∠D and ∠C=∠B.

View SolutionIn the given figure, Oa = OB and OC = OD. Which is the criteria to prove
ΔAOC≅ΔBOD.

View SolutionLet O be the origin and −−→OA=2ˆi+2ˆj+ˆk,−−→OB=ˆi−2ˆj+2ˆkand−−→OC=12(−−→OB−λ−−→OA) for same λ>0.If∣∣∣−−→OB×−−→OC∣∣∣=92 , then which of the following is(are) TRUE ?
View SolutionIn the figure given below, OD=OC=OB. Find ∠DCB.
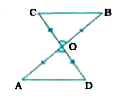
View SolutionIn the given figure, OA = OB and OD = OC. Show that
(i) ΔAOD≅ΔBOC and (ii) AD∣∣BC
View SolutionIn the given figure, ray OC is the bisector of ∠AOB and OD is the ray opposite to OC. Show that ∠AOD=∠BOD.

View Solution