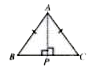
ABC is an isosceles triangle in which AB = AC. Prove that the tangent to the circum-circle at A is parallel to BC.
Step by step video & image solution for ABC is an isosceles triangle in which AB = AC. Prove that the tangent to the circum-circle at A is parallel to BC. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
ABC is an isosceles triangle with AB = AC. A circle through B touching AC at the middle point intersects AB at P. Then, AP : AB is
A3:5B1:4C4:1D2:3ABC is an isosceles triangle with AB = AC. A circle through B touching AC at the middle point intersects AB at P. Then AP : AB is :
A4:1B2:3C3:5D1:4
If ABC is an isosceles triangle with AB=AC. Prove that the perpendiculars from the vertices B and C to their opposite sides are equal.
View SolutionABC is an isosceles triangle right-angled at C. Prove that AB2=2AC2.
View SolutionABC is an isosceles triangle with AC = BC. If AB2=2AC2, prove that ABC is a right triangle.
View Solution△ABC is an isosceles triangle with AC = BC. If AB2=2AC2 . Prove that △ABC is a right triangle.
View SolutionIn a right angle triangle ΔABC is which ∠B=90∘ a circle is drawn with AB diameter intersecting the hypotenuse AC at P.Prove that the tangent to the circle at PQ bisects BC.
View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
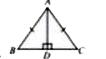
AD bisects BC
View Solution