In a right angle triangle ΔABC is which ∠B=90∘ a circle is drawn with AB diameter intersecting the hypotenuse AC at P.Prove that the tangent to the circle at PQ bisects BC.
BQ=PQ-(1)
∠APB=90o
∠BPC=180−90=90o
∠BPC=900
∠BPQ+∠QPC=90o
from equation 1
∠BPQ=∠PBQ
∠PBQ+∠PCQ=90o−(3)
from equation 2 and 3
∠BPQ+∠QPC=∠PBQ+∠PCQ
∠QPC=∠PCQ
PQ=QC
From 1
BQ=QC
Q is mid point of BC.
समान प्रश्न
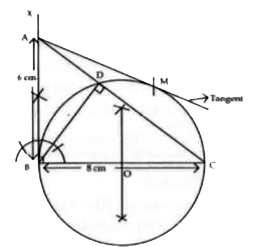
Let ABC be a right triangle in which AB=6cm,BC=8cm and ∠B=90∘. BD is the perpendicular from B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle.
View SolutionLet ABC be a right triangle in which AB = 6 cm, BC = 8 cm and ∠B=90∘. BD is the= perpendicular from B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle.
View SolutionIn a right-triangle ABC in which ∠B=90∘, a circle is drawn with AB as diameter intersecting the hypotenuse AC at P. Prove that the tangent to the circle at P bisects BC.
View SolutionLet ABC be a right-triangle in which AB = 6 cm, BC = 8 cm , and B=90∘. BD is the perpendicular from B on AC. A circle through B, C, D is drawn. Construct the tangent from A to this circle.
View SolutionIn a right angle triangle ΔABC is which ∠B=90∘ a circle is drawn with AB diameter intersecting the hypotenuse AC at P.Prove that the tangent to the circle at PQ bisects BC.
View SolutionIn ΔABC,AB=AC.A circle is drawn with diameter AB and it intersects BC at D. Prove that D is the midpoint of BC.
View SolutionA right angled triangle ABC, in which angle B = 90^(@) Is, a circle is drawn assuming AB as diameter, which intersects hypotenuse AC at P. Prove that the tangent line of the circle at P bisects BC.
View SolutionIn a right triangle ABC, a circle with AB as diameter is drawn to intersect the hypotenuse AC in P. Prove that the tangent at P, bisects the side BC.
View Solution
