BL and CM are medians of a triangle ABC right angled at A. Prove that 4(BL2+CM2)=5BC2.Solution in Telugu
Step by step video & image solution for BL and CM are medians of a triangle ABC right angled at A. Prove that 4(BL^2+CM^2)=5BC^2. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In △ABC, DE∣∣BC and AD=13BD.
If BC = 4.5cm, Find DE.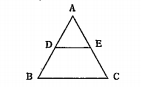
View SolutionWhich of the following are sets? Justify your answer.
The collection of all even integers.
View SolutionThe median of the data x/5, x, x/4, x/2 and x/8 is 8. Find the value of x.
View SolutionBL and CM are medians of a triangle ABC right angled at A. Prove that 4(BL2+CM2)=5BC2
View Solutionसमकोण त्रिभुज ABC जो A पर समकोण है और BL तथा CM माधिकाये है तथा BC = 5 cm है, यदि BL = 3√52 cm है, तब CM की लम्बाई ज्ञात करे?
View Solutionसमकोण त्रिभुज ABC में कोण A समकोण है और BL तथा CM उसक माध्यिकाएं हैं। सिद्ध कीजिए कि 4(BL2+CM2)=5BC2
View SolutionBL और CM एक समकोण त्रिभुज की माध्यिकाएँ हैं तथा इस त्रिभुज का कोण A समकोण है । सिद्ध कीजिए कि
4(BL2+CM2)=5BC2.
View SolutionBL and CM are medians of a triangle ABC right angled at A.
Prove that 4(BL2+CM2)=5BC2
View SolutionBL and CM are medians of a triangle ABC right angled at A. Prove that 4(BL2+CM2)=5BC2.
View SolutionIn Delta ABC, angle BAC = 90^(@), seg BL and seg CM are medians of Delta ABC prove that 4(BL^(2) + CM^(2)) = 5 BC^(2)
View SolutionBL மற்றும் CM செங்கோணம் A வில் உள்ள முக்கோணம் ABC ன் நடுக்கோடுகள் 4(BL2+CM2)=5BC2 என நிரூபிக்க ?
View SolutionBL and CM are medians of a triangle ABC right angled at A. Prove that 4(BL2+CM)2=5BC2 .
View SolutionBL and CM are medians of a triangle ABC right angled at A. Prove that 4(BL2+CM)2=5BC2 .
View SolutionBL and CM are medians of a triangle ABC right angled at A. Prove that 4(BL2+CM2)=5BC2
View SolutionBL and CM are medians of a DeltaABC right angled at A. Prove that 4(BL2+CM2)=5BC2.
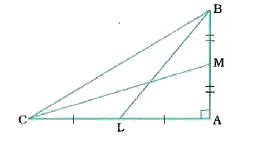
View SolutionBL and CM are medians of a DeltaABC right angled at A. Prove that 4(BL2+CM2)=5BC2.
View Solution
