In the following figure, BL=CM
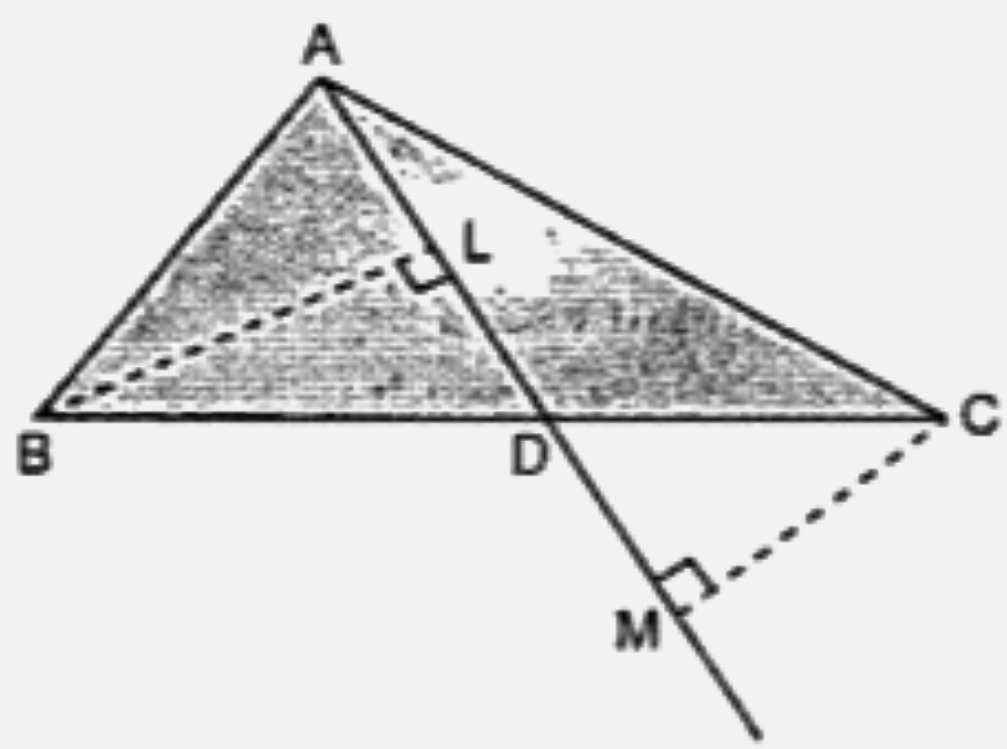
Prove that AD is a Median of triangle ABC
The correct Answer is:ΔABC.
Step by step video & image solution for In the following figure, BL=CM Prove that AD is a Median of triangle ABC by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLES BOOK - ICSECHAPTER - TRIANGLES EXERCISE - 4 MARKS QUESTIONS
24 Videos
- TRIANGLES BOOK - ICSECHAPTER - TRIANGLES EXERCISE - QUESTIONS
8 Videos
- STATISTICS AND GRAPH WORK BOOK - ICSECHAPTER - STATISTICS AND GRAPH WORK EXERCISE - TOPIC - 2 (4 Marks Questions)
14 Videos
- TRIGONOMETRICAL RATIOS BOOK - ICSECHAPTER - TRIGONOMETRICAL RATIOS EXERCISE - EXERCISE 22(B)
50 Videos
Similar Questions
In the following figures, the sides AB and BC and the median AD of triangle ABC are respectively equal to the sides PQ and QR and median PS of the triangle PQR. Prove that ΔABCandΔPQR are congruent.

View SolutionIn the given figure , CM and RN are respectively the median of triangles ABC and PQR

IF ΔABC is similar to ΔPQR ,prove that
(i) ΔAMC~ΔPNR
(ii) CMRN=ABPQand
(iii)ΔCMB~ΔRNQ
View SolutionProve that the medians of a triangle are concurrent.
View SolutionIn the following figure ABC is a right angled triangle with ∠BAC=90∘,andAD⊥BC.
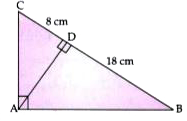
If BD = 18 cm, CD = 8 cm find AD.
View SolutionIn the following figure ABC is a right angled triangle with ∠BAC=90∘,andAD⊥BC.

(i) Prove ΔADB~ΔCDA.
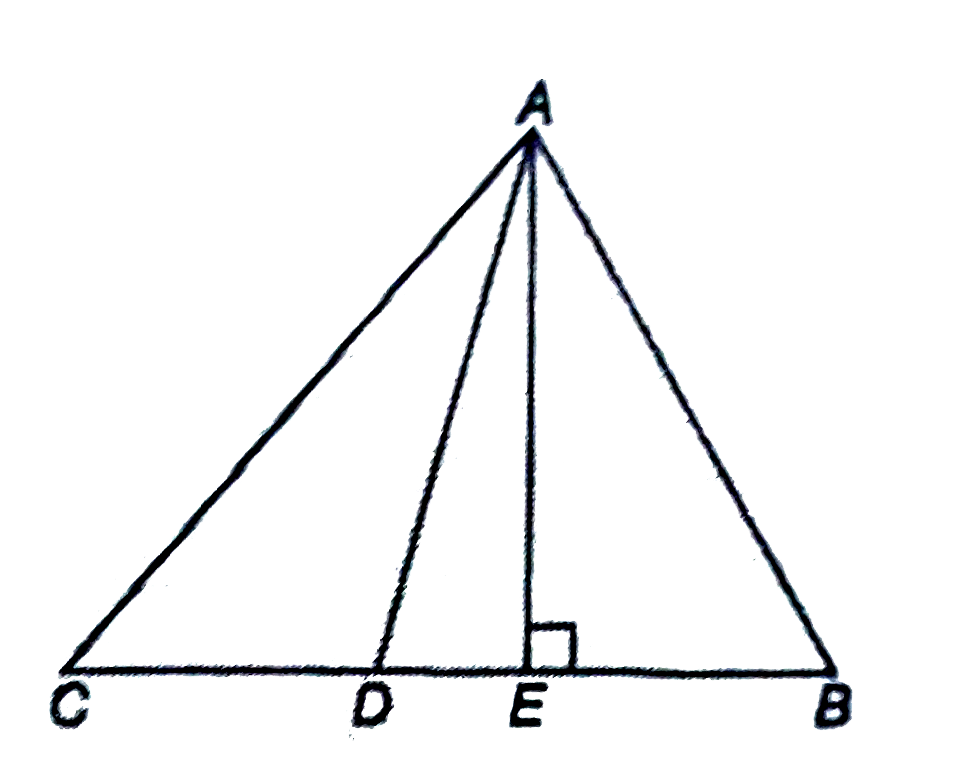
View SolutionThe following figure shows a triangle ABC in which AD is a median and AE⊥BC. Prove that 2AB2+2AC2=4AD2+BC2 .
View SolutionIn the following figure G, is centroid of the triangles ABC.
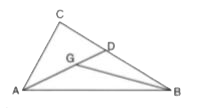
Prove that
Area (Δ AGB )=13× Area (ΔABC)
View SolutionIn the following figure, AD and CE are medians of ΔABC. DF is drawn parallel to CE. Prove that :
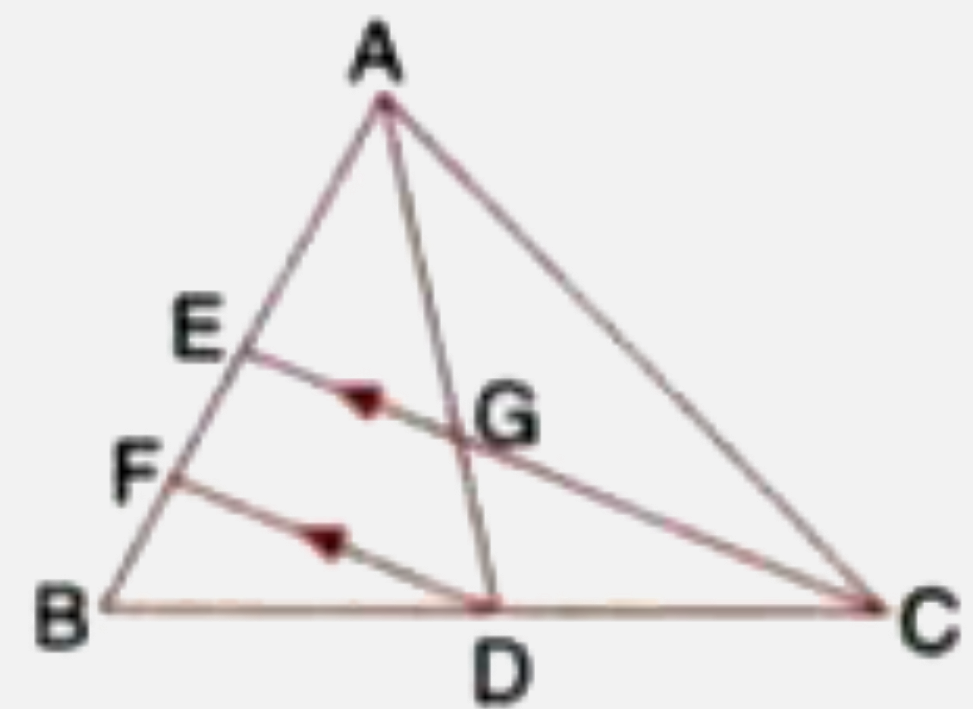
AG:GD=2:1.
View SolutionIn the following figure, AD and CE are medians of ΔABC. DF is drawn parallel to CE. Prove that :

EF=FB
View SolutionIn the adjoining figure, ΔABC is an isosceles triangles in which AB=AC and AD is a median. Prove that :
(i) ΔADB≅ΔADC
(ii) ∠BAD=∠CAD
View Solution
