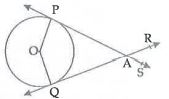
P and Q are two points ona circle with centre at O. R is a point on the minor arc of the circle, between the points P and Q. The tangents to the circle at the points P and Q meet each other at the points S. If ∠PSQ=20∘, then ∠PRQ =Solution in Bengali
80∘
200∘
160∘
100∘
Step by step video & image solution for P and Q are two points ona circle with centre at O. R is a point on the minor arc of the circle, between the points P and Q. The tangents to the circle at the points P and Q meet each other at the points S. If anglePSQ =20^@, then anglePRQ = by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- Theorems related to Cyclic quadrilateralBOOK - UNITED BOOK HOUSECHAPTER - Theorems related to Cyclic quadrilateralEXERCISE - Exercise
10 Videos
- Trigonometric Rations and Trigonometric IdentitiesBOOK - UNITED BOOK HOUSECHAPTER - Trigonometric Rations and Trigonometric IdentitiesEXERCISE - Exercise
31 Videos
Similar Questions
Multiple Choice Questions (MCQ) PQRS is a cyclic quadrilateral and PQ is a diameter of the circle. If ∠PSR=130∘ then ∠QPR =
View SolutionMultiple Choice Question (MCQ) Maximum value of cosθ is
View SolutionP तथा Q वृत्त पर दो बिंदु स्तिथ है तथा केंद्र O है। वृत्त की लघु चाप पर बिंदु R स्तिथ है। बिंदु P तथा Q पर खींची गई स्पर्श रेखाएं बिंदु S पर मिलती है। यदि ∠PSQ=20∘ है, तब ∠PRQ=?
View SolutionTwo circles touch each other at the point R. PQ is a common tangent to both the circle which touches the circle at the points P and Q. Then ∠PRQ=
View SolutionIn the figure, two circles intersect each other in points P and Q. If tangent from point R touch the circles at S and T, then prove that RS=RT.

View SolutionDraw a circle centre O. Take two points P and Q on the circle with such that ∠AOB=120∘. Draw tangents at points A and B.
View SolutionP and Q are two points on circle with centre O. The point R is on the minor arcPQ. The tangents from P and Q meet at S. If ∠PSQ=20∘ them ∠PRQ is-
View SolutionTwo circles touch each other externally at a point P and a direct common tangent touches the circles at the points Q and R respectively. Then ∠QPR is
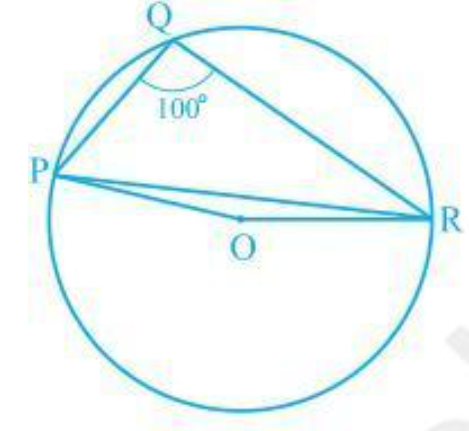
View Solution∠PQR=100∘, where P, Q and R are points on a circle with centre O. Find ∠OPR
View SolutionIf O If the point of the supporting circle of the ellipse is the corresponding point of P, then the points P and Q meet.
View SolutionA tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ=13cm . Find the length of PQ .
View SolutionA tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q such that OQ=12cm . Length PQ is
View SolutionPQ is a tangent to a circle with centre O at the point P . If △OPQ is an isosceles triangle, then ∠OQP is equal to :
View SolutionIn the figure, two circles intersect each other in points P and Q. If tangent from point R touch the circles at S and T, then prove that RS=RT.

View SolutionA circle with centre O. point A is the exterior of the circle. Line AP and line AQ are tangents at point P and point Q respectively P-A-S, Q-A-R, ∠PAR=130∘. Find ∠AOP
View Solution
