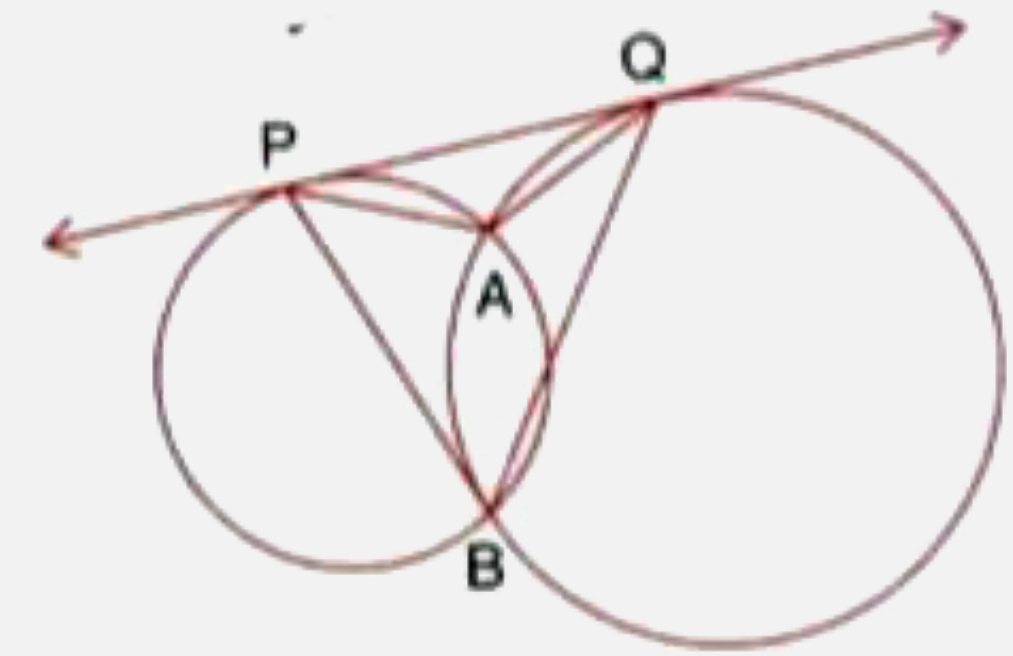
Two circles intersect each other at points A and B. A straight line PAQ cuts the circles at P and Q. If the tangents at P and Q intersect at point T, show that the points P, B, Q and T are concylic.
Step by step video & image solution for Two circles intersect each other at points A and B. A straight line PAQ cuts the circles at P and Q. If the tangents at P and Q intersect at point T, show that the points P, B, Q and T are concylic. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TANGENTS AND INTERSECTING CHORDSBook:ICSEChapter:TANGENTS AND INTERSECTING CHORDSExercise:EXERCISE 18 (C)
Explore 42 Videos
- TANGENTS AND INTERSECTING CHORDSBook:ICSEChapter:TANGENTS AND INTERSECTING CHORDSExercise:EXERCISE 18(A)
Explore 24 Videos
- SPECIMEN QUESTION PAPER (MATHEMATICS)Book:ICSEChapter:SPECIMEN QUESTION PAPER (MATHEMATICS)Exercise:Section C
Explore 12 Videos
- TRIGONOMETRICAL IDENTITIESBook:ICSEChapter:TRIGONOMETRICAL IDENTITIESExercise:QUESTIONS
Explore 22 Videos
Similar Questions
Two equal circles intersect in P and Q . A straight line through P meets the circles in A and B . Prove that QA=QB.
View SolutionTwo equal circles intersect in P and Q . A straight line through P meets the circles in A and B . Prove that QA=QB.
View SolutionTwo circles intersects in points P and Q. A secant passing through P intersects the circles in A and B respectively. Tangents to the circles at A and B intersect at T. Prove that the A,Q,B and T lie on a circle.
View SolutionTwo circles intersect each other at point A and B. Their common tangent touches the circles at points P and Q as shown in the figure. Show that the angles PAQ and PBQ are supplementary.
View SolutionPQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T . Find the length TP .
View SolutionIn the figure, two circles intersect each other at points A and B. AP and AQ are the diameters of these circels. Prove that PBQ is a straight line.

View SolutionIn the figure, two circles intersect each other at points A and B. AP and AQ are the diameters of these circels. Prove that PBQ is a straight line.

View SolutionTwo circles touch each other extermally at point P. APC and BPD are straight lines. Show that :
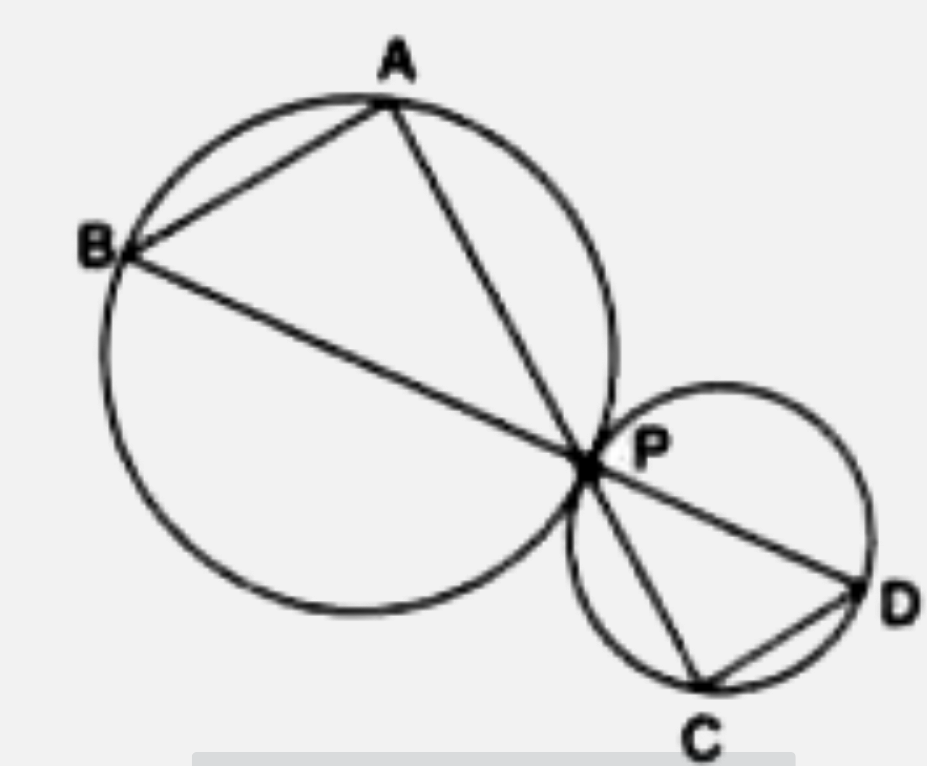
AP is parallel to CD.
View SolutionTwo congruent circles intersect each other at points A and B. Through A any linesegment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
View SolutionIn Figure, two circles touch each other at the point C . Prove that the common tangent to the circles at C , bisects the common tangent at P and Q .
View Solution