N is the foot of the perpendicular form P to the diameter AB of the circle APB. P lies on the circle APB. Prove that PB2=AB.NB,Solution in Bengali
Step by step video & image solution for N is the foot of the perpendicular form P to the diameter AB of the circle APB. P lies on the circle APB. Prove that PB^2=AB.NB, by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Price of a machine is Rs 2,00,000. The price of it decrease in 1st year and 2nd year by 15% and 10% respectively. The price of the machine will be after 2 years is
View SolutionCompound interest and simple interest of sun of money at the same rate of interest per annum are equal in
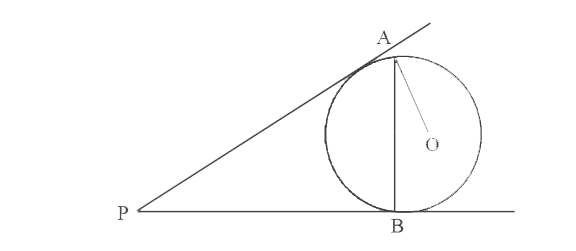
View SolutionFrom a point P , two tangents PA and PB are drawn to a circle with centre O . If OP= diameter of the circle, show that APB is equilateral.
View Solutionएक वृत्त C(O, r) पर एक बिन्दु P से दो स्पर्शियाँ PA व PB खींची गयी है । यदि OP = 2r । सिद्ध कीजिए कि ΔAPB एक समबाहु त्रिभुज है।
View SolutionAB एक वृत्त का एक व्यास है । अर्धवृत्त APB पर P एक बिंदु है| P से गुजरने वाली स्पर्श रेखा पर A तथा B एक लम्ब क्रमशः AH तथा BK हैं| सिद्ध करें कि AH+BK=AB है|
View SolutionTwo tangents PA and PB are drawn to a circle with centre O from an external point P. Prove that ∠APB=2∠OAB
View SolutionO வை மையமாக உடைய வட்டத்திற்கு வெளியே உள்ள புள்ளி P யிலிருந்து வரையப்பட்ட தொடுகோடுகள் PA மற்றும் PB ஆகும் ∠APB =70∘ எனில் ∠AOB -யின் மதிப்பு காண்க ?
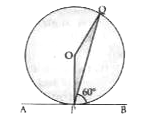
View SolutionAPB is tangent at P to the circle with centres O.If ∠QPB=60∘,then ∠POQ is :
View SolutionAB is a diameter of circle. P is a point on the semicircle APB. AH and BK are perpendiculars from A and B respectively to the tangents at P. Prove that AH+BK=AB.
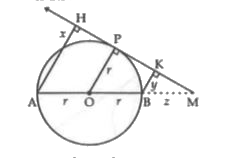
View Solutionवृत्त APB का व्यास AB है तथा A एवं B बिदु से P की स्पर्श रेखा पर AH तथा BK लांब खींचे गए हों तो सिद्ध करें कि AH+ BK= AB.
View SolutionAB Is a fixed line segment. Prove that the point P The locus of will be a circle whose diameter AB Is if angle APB = 90° Ho.
View SolutionIn the given figure, two circles touch each other externally at point P. AB is the direct common tangent of these circles. Prove that:
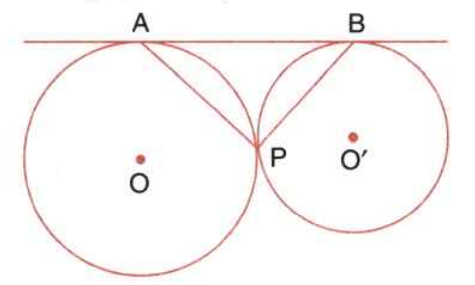
(i) tangent at point P bisects AB
(ii) angle APB=90∘
View SolutionO is the centre of a centre having diameter AB. P is any point on the circle. Draw a perpendicular from P to AB, which meets AB at N. Prove that PB2=AB.BN
View SolutionAB is a diameter of circle. P is point on circle and a perpendicular line is drawn on AB at N from it. If radius is 7 cm. and PB = 12 cm. then BN is (in cm)-
View SolutionOn a diameter AB of a circle, the foot of the perpendicular from the point P of a circle of radius 7 cm is N. If the length of chord PB is 12 cm. Then the distance (in cm) of N from point B is-
View Solution
