A plumber can be paid under two schemes as given below: I Rs. 600 and Rs 50 per hour II. Rs. 170 per hour. If the job takes n hours, for wht values of n does the scheme I gives the plumber the better wages?
To solve the problem, we need to compare the wages from the two schemes based on the number of hours worked (n).
1. Define the Wages for Each Scheme:
- Scheme I: The plumber earns Rs. 600 plus Rs. 50 for each hour worked. Therefore, the total wage for Scheme I can be expressed as:
W1=600+50n
- Scheme II: The plumber earns Rs. 170 for each hour worked. Thus, the total wage for Scheme II is:
W2=170n
2. Set Up the Inequality:
- We want to find the values of n for which Scheme I provides better wages than Scheme II. This can be expressed as:
W1>W2
- Substituting the expressions for W1 and W2:
600+50n>170n
3. Rearranging the Inequality:
- To isolate n, we first subtract 50n from both sides:
600>170n−50n
- This simplifies to:
600>120n
4. Dividing Both Sides by 120:
- To solve for n, divide both sides by 120:
600120>n
- Simplifying the left side gives:
5>n
- This can also be written as:
n<5
5. Conclusion:
- Therefore, Scheme I gives the plumber better wages when the number of hours worked n is less than 5.
Final Answer:
The scheme I gives the plumber better wages for values of n<5.
---
- Scheme I: The plumber earns Rs. 600 plus Rs. 50 for each hour worked. Therefore, the total wage for Scheme I can be expressed as:
W1=600+50n
- Scheme II: The plumber earns Rs. 170 for each hour worked. Thus, the total wage for Scheme II is:
W2=170n
- We want to find the values of n for which Scheme I provides better wages than Scheme II. This can be expressed as:
W1>W2
- Substituting the expressions for W1 and W2:
600+50n>170n
- To isolate n, we first subtract 50n from both sides:
600>170n−50n
- This simplifies to:
600>120n
- To solve for n, divide both sides by 120:
600120>n
- Simplifying the left side gives:
5>n
- This can also be written as:
n<5
- Therefore, Scheme I gives the plumber better wages when the number of hours worked n is less than 5.
The scheme I gives the plumber better wages for values of n<5.
Similar Questions
An electrician can be paid under two schemes as given below: I: Rs. 500 and Rs. 70 per hour. II: Rs. 120 per hour. If the job takes x hours, for what values of x does the i. Scheme I ii. Scheme II give the electrician the better wages.
View SolutionA small firm manufactures necklaces and bracelets. The total number of necklaces and bracelets that it can handle per day is at most 24. It takes 1 hour to make a bracelet and half an hour to make a necklace. The maximum number of hours available per day is 16. If the profit on a necklace is Rs 100 and that on a bracelet is Rs 300, how many of each should be produced daily to maximize the profit?
View SolutionA manufacturer produces two types of steel trunks. He has tow machines A and B. For completing, the first types of the trunk requires 3 hours on machine A and 3 hours on machine B, whereas the second type of the trunk requires 3 hours on machine A and 2 hours on machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit of Rs. 30 and Rs. 25 per trunk of the first type and the second respectively. How many trunks of each type must he make each day to makes maximum profit?
View SolutionA company sells two different products A and B. The two products are produced in a common production process and are sold in two different markets. The production process has a total capacity of 45000 man-hours. It takes 5 hours to produce a unit of A and 3 hours to produce a unit of B. The market has been surveyed and company officials feel that the maximum number of units of A that can be sold is 7000 ad that of B is 10,000. If the profit is Rs. 60 per unit for the product A and Rs. 40 per unit for the product B, how many units of each product should be sold to maximize profit? Formulate the problem as LPP.
View SolutionA manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the time (in minutes) required for each purpose and the time (in minutes) required for each toy on the machines is given below:
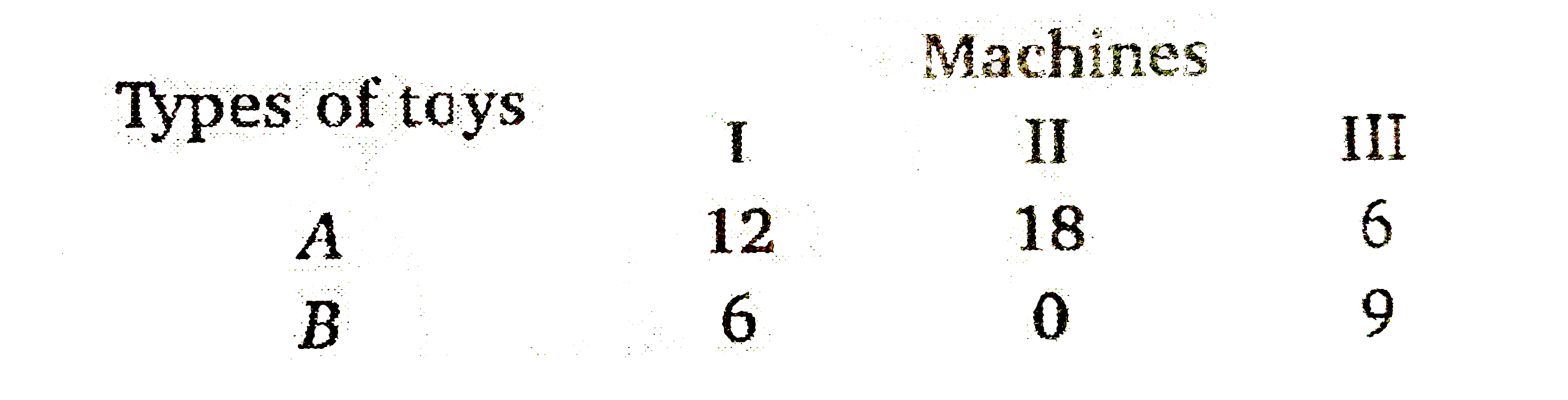
Each machine is available for a maximum of 6 hours per day. If the profit on each toy of type A is Rs. 7.50 and that on each toy of type B is Rs. 5, show that 15 toys of type A and 30 of type B should be manufactured in a day to get maximum profit.
View SolutionA manufacturer manufactures two types of tea-cups, A and B. Three machines are needed for manufacturing the tea cups. The time in minutes required for manufacturing each cup on the machines is given below:
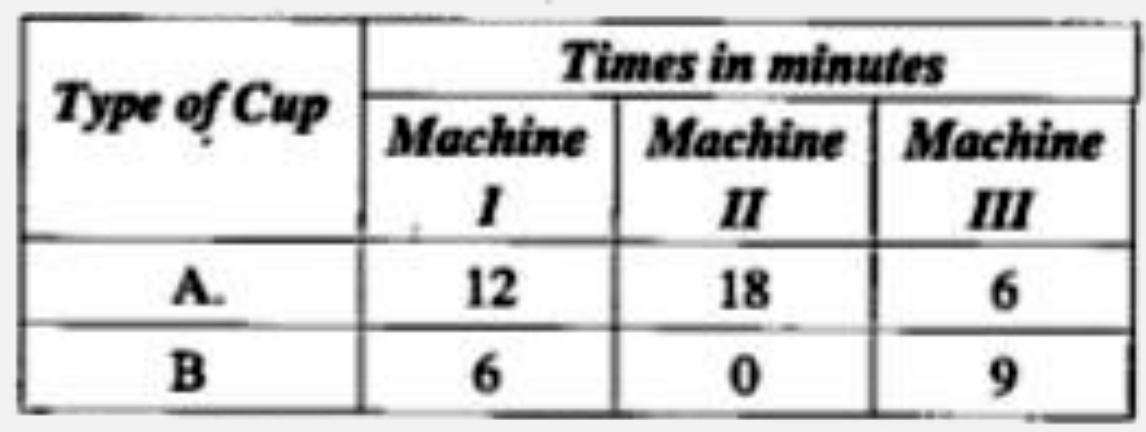
Each machine is available for a maximum of six hours per day. If the profit on each cup of type A is Rs 1.50and that'on each cup of type B is Rs 1.00, find the number of cups of each type that should be manufactured in a day to get maximumprofit.
View SolutionTo promote making of toilets for women, an organisation tried to generate awareness attempt (i) house calls (ii) letters, and (iii) announcements. The cost for each mode per attempt is given below: (i) Rs 50 (ii) Rs 20 (iii) Rs 40 The number of attempts made in three villages X, Y and Z are given below: (i) (ii) (iii) X 400 300 100 Y 300 250 75 Z 500 400 150 Find the total cost incurred by the organisation for three villages separately, using matrices.
View SolutionA manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of Rs 17.50 per package on nuts and Rs 7.00 per package on bolts. How many packages of each should be produced each day so as to maximise his profit, if he operates his machine for at most 12 hours a day?
View SolutionThe reduction is speed, r in miles per hour of an enginge having n bogies attached to it is given as : r=4√n. The final speed, s, in miles per hour , at which the engine can pull the n bogies attached is give as : s=40−r . What is the maximum number of bogies that the engine call pull ?
View SolutionA company sells two different products, A and B. The two products are produced in a common production process, which has a total capacity of 500 man-hours. It takes 5 hours to produce a unit of A and 3 hours to produce a unit of B. The market has been surveyed and company officials feel that the maximum number of units of A that can be sold is 70 and that, for B is 125. If the profit is Rs. 20 per unit for the product A and Rs. 15 per unit for the product B, how many units of each product should be sold to maximize profit?
View Solution
