Find the first negative termof the sequence 2000, 1995, 1990, 1985,……
To find the first negative term of the sequence 2000, 1995, 1990, 1985, ..., we can follow these steps:
Step 1: Identify the first term and common difference
The first term (A) of the sequence is:
A=2000
The common difference (D) can be calculated as:
D=1995−2000=−5
Step 2: Write the formula for the nth term
The formula for the nth term (a_n) of an arithmetic progression (AP) is given by:
an=A+(n−1)⋅D
Substituting the values of A and D, we get:
an=2000+(n−1)(−5)
Step 3: Set the nth term less than zero
To find the first negative term, we need to set the nth term less than zero:
2000+(n−1)(−5)<0
Step 4: Solve the inequality
Rearranging the inequality:
2000−5(n−1)<0
2000−5n+5<0
2005−5n<0
Now, isolating n:
−5n<−2005
Dividing both sides by -5 (remember to reverse the inequality):
n>401
Step 5: Find the smallest integer n
Since n must be an integer, the smallest value for n that satisfies this inequality is:
n=402
Step 6: Calculate the 402nd term
Now, we can find the 402nd term using the formula:
a402=2000+(402−1)(−5)
a402=2000+401⋅(−5)
a402=2000−2005
a402=−5
Conclusion
Thus, the first negative term of the sequence is:
First negative term=−5
---
The first term (A) of the sequence is:
A=2000
D=1995−2000=−5
The formula for the nth term (a_n) of an arithmetic progression (AP) is given by:
an=A+(n−1)⋅D
Substituting the values of A and D, we get:
an=2000+(n−1)(−5)
To find the first negative term, we need to set the nth term less than zero:
2000+(n−1)(−5)<0
Rearranging the inequality:
2000−5(n−1)<0
2000−5n+5<0
2005−5n<0
Now, isolating n:
−5n<−2005
Dividing both sides by -5 (remember to reverse the inequality):
n>401
Since n must be an integer, the smallest value for n that satisfies this inequality is:
n=402
Now, we can find the 402nd term using the formula:
a402=2000+(402−1)(−5)
a402=2000+401⋅(−5)
a402=2000−2005
a402=−5
Thus, the first negative term of the sequence is:
First negative term=−5
Similar Questions
Knowledge Check
Let S be the sum of the first n terms of the arithmetic sequence 3, 7, 11, ...., and let T be the sum of the first n terms of the arithmetic sequence 8 , 10 , 12 ,.... For n > 1 , S = T for
Ano value of nBone value of nCtwo values of nDthree values of n
Find the first five terms of the sequence for which t1=1,t2=2andtn+2=tn+tn+1
View SolutionFind the first 4 terms and the 20th term of the sequence whose
Sn=32(3n−1).
View SolutionIf tn=2nn+1, find the first five terms of the sequence.
View SolutionThe sequence 9,18,27,36,45,54,….. consists of successive mutiple of 9. This sequence is then altered by multiplying every other term by −1, starting with the first term, to prduce the new sequence −9,18,−27,36,−45,54,…….. If the sum of the first n terms of this new sequence is 180, determine n.
View SolutionFind product in reaction sequence
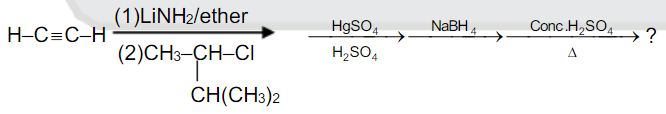
View SolutionFind the first four terms of the sequence defined by a1=3 and an=3an−1+2 , for all n.1.
View SolutionFind the first four terms of the sequence defined by a1=3 and an=3an−1+2 , for all n>1.
View Solution
