Let the sequence {bn} real numbers satisfies the recurrence relation bn+1=13(2bn+125(bn)2),bn≠0. Then find the (lim)n→∞bn.Solution in Tamil
Step by step video & image solution for Let the sequence {b_n} real numbers satisfies the recurrence relation b_(n+1)=1/3(2b_n+(125)/(b_n)^2),b_n!=0. Then find the (lim)_(n to oo)b_ndot by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Complete the following statements.
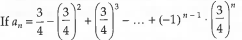 and bn=1−an then the smallest natural number n0, such that bn>anVntn>n0 is
and bn=1−an then the smallest natural number n0, such that bn>anVntn>n0 is
View SolutionLet An=(34)−(34)2+(34)3+.....+(−1)n−1(34)n , B_n = 1 - A_n . Find a least odd natural number n0, so that Bn>An∀n≥n0.
View SolutionLet f(x)=a_0+a_1x+a_2x^2++a_n x^n+ and (f(x))/(1-x)=b_0+b_1x+b_2x^2++b_n x^n+ , then b_n+b_(n-1)=a_n b. b_n-b_(n-1)=a_n c. b_n//b_(n-1)=a_n d. none of these
View SolutionIf a_n and b_n are positive integers and a_n+sqrt(2)b_n=(2+sqrt(2))^n ,t h e n(lim)_(x->oo)((a_n)/(b_n))= a. 2 b. sqrt(2) c. e^(sqrt(2)) d. e^2
View SolutionIf an=34−(34)2+(34)3+...(−1)n−1(34)n and bn=1−an, then find the minimum natural number n, such that bn>an
View SolutionIf an=34−(34)2+(34)3+...(−1)n−1(34)n and bn=1−an, then find the minimum natural number n, such that bn>an
View SolutionIf An=∫π20sin(2n−1)xsinxdx,Bn=∫π20(sinnxsinx)2dx for n∈N, Then
(A) An+1=An (B) Bn+1=Bn (C) An+1−An=Bn+1 (D) Bn+1−Bn=An+1
View Solution