(a) Draw the graph of f(x)==⎧⎪
⎪⎨⎪
⎪⎩1,|x|≥11n2,1n<|x|<1n−1,n=2,3,...0,x=0
(b) Sketch the region y≤−1.
(c) Sketch the region |x|<3. Solution in Tamil
(a) f(x)==⎧⎪
⎪⎨⎪
⎪⎩1,|x|≥11n2,1n<|x|<1n−1,n=2,3,...0,x=0
=⎧⎪
⎪
⎪
⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪
⎪
⎪
⎪⎩1,x≤−1orx≥114,x∈(−1,−12)∪(12,1)19,x∈(−12,−13)∪(13,12)...
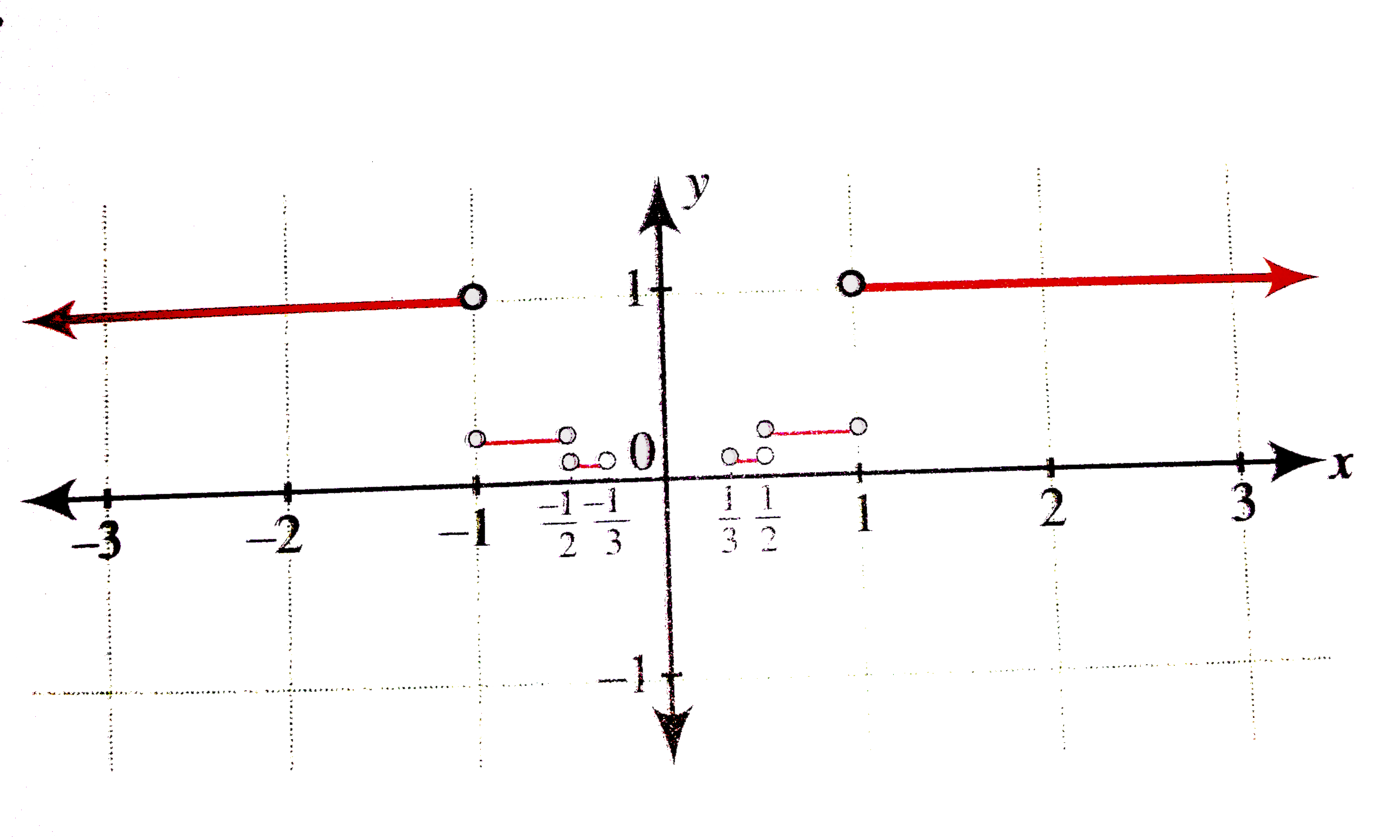
(b) y≤−1
For y≤−1, first draw the line y=−1. All the points satisfying y≤−1 have ordinate greater than, or equal to, -1, i.e. all the points lying on or below the line y=−1.
The region is as shown in the following region.

(c ) |x|<3
So −3<x<3, i.e. all points have abscissae lying between -3 and 3. Hence all the points lying between the lines x=−3andx=3.

Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise34videos
GRAPHS OF ELEMENTARY FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises4videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
Similar Questions
Draw the graph of y=1(1/x).
View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=001:56View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
03:04View Solution(a) Draw the graph of f(x)==⎧⎪ ⎪⎨⎪ ⎪⎩1,|x|≥11n2,1n<|x|<1n−1,n=2,3,...0,x=0
(b) Sketch the region y≤−1.
(c) Sketch the region |x|<3.View SolutionThe number of real roots of the equation
1+a1x+a2x2+………..anxn=0, where |x|<13 and |an|<2, is13:45View SolutionIf 0<x<π2 and sinnx+cosnx≥1, then
05:47View SolutionThe function f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩1|x|≤11n21n≤|x|<1n−1,n=2,3,...0x=0
03:52View SolutionFor each ositive integer n, define a function fnon[0,1] as follows:
fn⎛⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜⎝(x)=⎧⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎩0ifx=0sinπ2nif0<x≤1nsin2π2nif1n<x≤2nsin3π2πif2n<x≤3nsin'nπ2πifn−1n<x≤1 Then the value of limx→∞∫10fn(x)dx is:View SolutionLtx→0(1x+2x+3x+....+nxn)1/x)
01:20View Solutionf(x)=⎧⎪⎨⎪⎩[x] if −3<x≤−1[x] if −1<x<|[−x]| if 1≤x<3 then {x:f(x)≥0} is equal to :
01:10View SolutionIf f(x)=⎧⎪⎨⎪⎩[x],if−3<x≤−1|x|,if−1<x<1|[x]|,if1≤x<3
then the set {x:f(x)≥0} is equal to07:23View SolutionSketch the graph of y=sin(13x) for 0≤x<6π.
03:13View SolutionThe number of real roots of :
1+a1X+a2x2....+anxn=0, where |x|<13 and |an|<2, is :06:54View Solution(a) Draw the graph of f(x)==⎧⎪ ⎪⎨⎪ ⎪⎩1,|x|≥11n2,1n<|x|<1n−1,n=2,3,...0,x=0
(b) Sketch the region y≤−1.
(c) Sketch the region |x|<3.02:26View Solutionf(x)=⎧⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪⎩12−x,0≤x<121,x=1232−x,12<x≤1 Discuss the continuity of f(x)
04:35View Solutionf(x)=⎧⎪⎨⎪⎩[x]if−3<x≤−1|x|if−1<x<1|[−x]|if1≤x≤3, then {x:f(x)≥0}=
16:04View Solution

