Line segment AB of fixed length c slides between coordinate axes such that its ends A and B lie on the axes. If O is origin and rectangle OAPB is completed, then show that the locus of the foot of the perpendicular drawn from P to AB is x23+y23=c23.
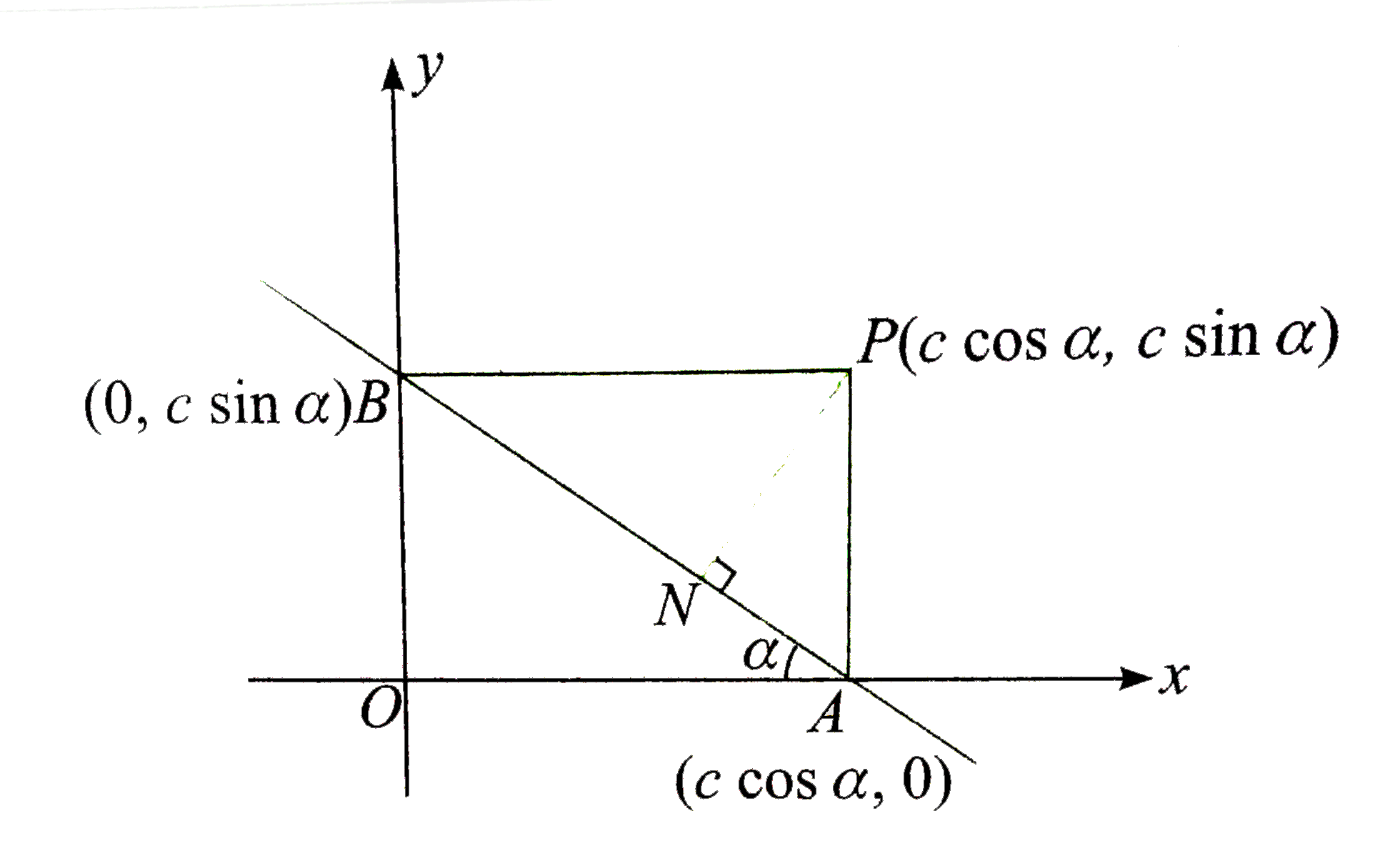
As shown in the figure, is on x-axis and B is on y-axis.
AB=c (given)
Given that OAPB is a rectangle.
Let ∠BAO=α
∴OA=ccos αandOB= c sin α
∴P≡(ccos α,csin α)
Equation of AB is
xc cos α+ycsin α=1
orxsin α+ycosα=c sinαcosα (1)
Equation of PN (perpendicular from P to AB) is
y−csinα=cota(x−ccosα)
⇒xcosα−ysinα=c(cos2α−sin2α) (2)
N is point of intersection of (1) and (2).
Solving (1) and (2), we get
x=ccos3α,y=csin3α
∴cosα=(xc)1/3,sinα=(yc)1/3
Squaring and adding, we get
(xc)2/3+(yc)2/3=1
orx2/3+y2/3=c2/3,which is the required locus
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.1
23 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.2
4 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year
9 Videos
Similar Questions
The ends A and B of a straight line segment of constant length c slide upon the fixed rectangular axes OX and OY, respectively. If the rectangle OAPB be completed, then the locus of the foot of the perpendicular drawn from P to AB is
View SolutionThe ends A and B of a straight line segment of constant length c slide upon the fixed rectangular axes OX and OY, respectively. If the rectangle OAPB be completed, then the locus of the foot of the perpendicular drawn from P to AB is
View Solution
Knowledge Check
If a circle of radius R passes through the origin O and intersects the coordinate axes at A and B, then the locus of the foot of perpendicular from O on AB is
A(x2+y2)2=4R2x2y2B(x2+y2)3=4R2x2y2C(x2+y2)(x+y)=R2xyD(x2+y2)2=4Rx2y2If a circle of radius R passes through the origin O and intersects the coordinates axes at A and B, then the locus of the foot of perpendicular from O on AB is:
A(x2+y2)(x+y)=R2xyB(x2+y2)3=4R2x2y2C(x2+y2)2+4Rx2y2D(x2+y2)=4R2x2y2
The straight line through a fixed point (2,3) intersects the coordinate axes at distinct point P and Q. If O is the origin and the rectangle OPRQ is completed then the locus of R is
View SolutionThe straight line through a fixed point (2,3) intersects the coordinate axes at distinct point P and Q. If O is the origin and the rectangle OPRQ is completed then the locus of R is
View SolutionThe ends A and B of a straight line segment of constant length c slide upon the fixed rectangular axes OX and OY, respectively. If the rectangle OAPB be completed, then the locus of the foot of the perpendicular drawn from P to AB is
View SolutionA circle of constant radius r passes through the origin O and cuts the axes at A and B. Show that the locus of the foot of the perpendicular from O to AB is (x2+y2)2(x−2+y−2)=4r2.
View SolutionA circle of constant radius r passes through the origin O and cuts the axes at A and B. Show that the locus of the foot of the perpendicular from O to AB is (x2+y2)2(x−2+y−2)=4r2.
View SolutionA rod of length k slides in a vertical plane, its ends touching the coordinate axes. Prove that the locus of the foot of the perpendicular from the origin to the rod is (x2+y2)3=k2x2y2.
View Solution
