A line $L$ is a drawn from $P (4, 3)$ to meet the lines $L - 1 a n d L_{2}$ given by $3 x + 4 y + 5 = 0$ and $3 x + 4 y + 15 = 0$ at points $A a n d B$ , respectively. From $A$ , a line perpendicular to $L$ is drawn meeting the line $L_{2}$ at $A_{1} .$ Similarly, from point $B_{1} .$ Thus, a parallelogram $\forall_{1} B B_{1}$ is formed. Then the equation of $L$ so that the area of the parallelogram $\forall_{1} B B_{1}$ is the least is $x - 7 y + 17 = 0$ $7 x + y + 31 = 0$ $x - 7 y - 17 = 0$ $x + 7 y - 31 = 0$

Text Solution

Verified by Experts

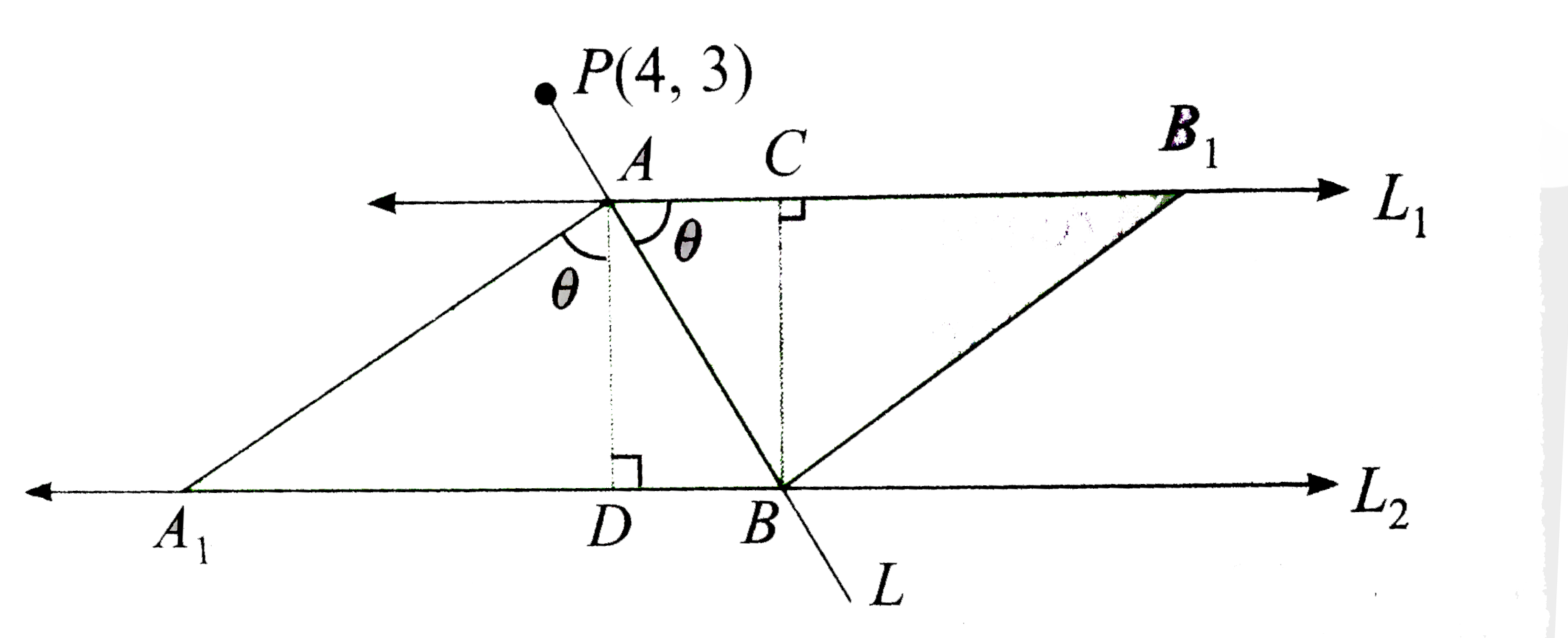
The given lines $(L_{1} and L_{2})$ are parallel and the distance between them (BC or AD) is (15-5)/5 = 0 units. Let $∠ B A C = θ .$ So, AB = BC cosec $θ = 2$ cosec $θ {and AA}_{1} = A D sec θ = 2 sec θ .$ Now, the area of parallelogram ${AA}_{1} B B_{1}$ is
$Δ = A B \times {AA}_{1} = 4 sec θ cosec θ$
$= \frac{8}{sin 2 θ}$
$Clearly, Δ is the least for θ = π / 4 . Let the slope of AB be m. Then,$
${tan 45}^{\circ} = ∣ ∣ ∣ \frac{m + 3 / 4}{1 - (3 m / 4)} ∣ ∣ ∣$
$or 4 m + 3 = \pm (4 - 3 m) or m = \frac{1}{7} or - 7$
Hence, the equation of L is
x-7y+17=0
or 7x + y -31=0

|

Updated on:21/07/2023

Class 12 MATHS STRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A variable line L is drawn through O(0,0) to meet the line $L_{1} and L_{2}$ given by y-x-10 =0 and y-x-20=0 at Points A and B, respectively.
Locus of P, if $O P^{2} = O A \times O B$ , is
A ${(y - x)}^{2} = 100$
B ${(y + x)}^{2} = 50$
C ${(y - x)}^{2} = 200$
Dnone of these
Question 2 - Select One
The three lines $l_{1} = 4 x - 3 y + 2 = 0, l_{2} = 3 x + 4 y - 4 = 0$ and $l_{3} = x - 7 y + 6 = 0$
Aform a rt. angled isosceles triangle
Bform a rt. Angled triangle
Care concurrent
DNone

CENGAGE-STRAIGHT LINES-JEE Advanced Previous Year

Home
Ask Doubt
Profile